Question

【题目】如图，已知AB是⊙O的直径，点E在⊙O上，过点E的直线EF与AB的延长线交与点F，AC⊥EF，垂足为C，AE平分∠FAC．

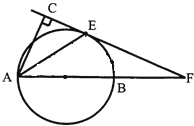
（1）求证：CF是⊙O的切线；

（2）∠F=30°时，求的值？

Answer 1

【答案】（1）证明见解析（2）

【解析】试题分析：（1）连接OE，根据角平分线的性质和等边对等角可得出OE∥AC，则∠OEF=∠ACF，由AC⊥EF，则∠OEF=∠ACF=90°，从而得出OE⊥CF，即CF是⊙O的切线；

（2）由OE∥AC，则△OFE∽△AFC，根据相似三角形的面积之比等于相似比的平方，从而得出的值．

试题解析：（1）连接OE，

∵AE平分∠FAC，

∴∠CAE=∠OAE，

又∵OA=OE，∠OEA=∠OAE，∠CAE=∠OEA，

∴OE∥AC，

∴∠OEF=∠ACF，

又∵AC⊥EF，

∴∠OEF=∠ACF=90°，

∴OE⊥CF，

又∵点E在⊙O上，

∴CF是⊙O的切线；

（2）∵∠OEF=90°，∠F=30°，

∴OF=2OE，

又OA=OE，

∴AF=3OE，

又∵OE∥AC，

∴△OFE∽△AFC，

∴，

∴，

∴