
【题目】如图,已知∠COA=90°,∠COD比∠DOA大28°,且OB是∠COA的平分线.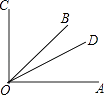
(1)求∠BOD的度数;
(2)将已知条件中的28°改为32°,则∠BOD=;
(3)将已知条件中的28°改为n°,则∠BOD= .
【答案】
(1)解:∵∠COD比∠DOA大28°,
∴∠COD=∠DOA+28°,
∵∠AOC=90°,
∴∠COD+∠DOA=90°,
∴∠DOA+28°+∠DOA=90°,
∴∠DOA=31°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC
= ![]() ∠AOC
∠AOC
=45°,
∴∠BOD=∠AOB﹣∠DOA
=45°﹣31°
=14°
(2)16°
(3)( ![]() )°
)°
【解析】解: (2)∵∠COD比∠DOA大32°,
∴∠COD=∠DOA+32°,
∵∠AOC=90°,
∴∠COD+∠DOA=90°,
∴∠DOA+32°+∠DOA=90°,
∴∠DOA=29°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC
= ![]() ∠AOC
∠AOC
=45°,
∴∠BOD=∠AOB﹣∠DOA
=45°﹣29°
=16°;
故答案为:16°;(3)∵∠COD比∠DOA大n°,
∴∠COD=∠DOA+n°,
∵∠AOC=90°,
∴∠COD+∠DOA=90°,
∴∠DOA+n°+∠DOA=90°,
∴∠DOA=(45﹣ ![]() )°,
)°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC
= ![]() ∠AOC
∠AOC
=45°,
∴∠BOD=∠AOB﹣∠DOA
=45°﹣(45﹣ ![]() )°
)°
=( ![]() )°;
)°;
故答案为:( ![]() )°.
)°.
(1)根据已知条件可求∠AOB和∠DOA,而∠BOD=∠AOB﹣∠DOA;(2)方法同(1);(3)方法同(1)。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(3,4),C(4,﹣1).
(1)试在平面直角坐标系中,画出△ABC; 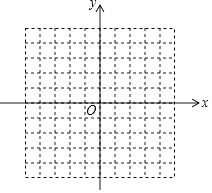
(2)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标;
(3)在x轴上找到一点P,使点P到点A、B两点的距离和最小;
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠a.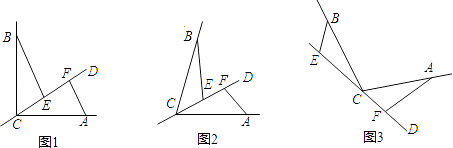
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图l,若∠BCA=90°,∠a=90°,则BECF;EF|BE﹣AF|(填“>”,“<”或“=”);
②如图(2),若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件 , 使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F. 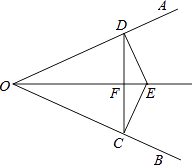
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]()
(1)填空:AB= , BC=;
(2)若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动.试探索:BC﹣AB的值是否随着时间的变化而改变?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知C为线段AB的中点,D为线段AC的中点.
(1)画出相应的图形,求出图中线段的条数并写出相应的线段;
(2)若图中所有线段的长度和为26,求线段AC的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com