
【题目】已知C为线段AB的中点,D为线段AC的中点.
(1)画出相应的图形,求出图中线段的条数并写出相应的线段;
(2)若图中所有线段的长度和为26,求线段AC的长度.
【答案】
(1)解:如图:![]()
图中共有6条线段,它们是线段AD、线段AC、线段AB、线段DC、线段DB、线段CB
(2)解:设线段AC的长度为x.
∵点C为线段AB的中点,
∴AC=BC= ![]() AB,
AB,
∴BC=x,AB=2AC=2x.
又∵点D为线段AC的中点,
∴AD=DC= ![]() AC=
AC= ![]() x.
x.
∵图中所有线段的长度和为26,
∴ ![]() x+x+2x+
x+x+2x+ ![]() x+(
x+( ![]() x+x)+x=26,
x+x)+x=26,
即6 ![]() x=26,
x=26,
∴x=4.
答:若图中所有线段的长度和为26,求线段AC的长度为4
【解析】(1)根据题意直接画出图形即可,利用图形直接写出所有的线段即可 ;
(2)设线段AC的长度为x,根据C为线段AB的中点,D为线段AC的中点,可用x表示出所有的线段长度,结合所有线段的长度和为26列出方程,解出方程即可.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠COA=90°,∠COD比∠DOA大28°,且OB是∠COA的平分线.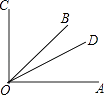
(1)求∠BOD的度数;
(2)将已知条件中的28°改为32°,则∠BOD=;
(3)将已知条件中的28°改为n°,则∠BOD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解2014年我市参加中考的334000名学生的视力情况,从中抽查了1000名学生的视力情况进行统计分析,下面判断正确的是( )
A.334000名学生是总体
B.每名学生是总体的一个个体
C.1000名学生的视力情况是总体的一个样本
D.上述调查是普查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a=255 ,b=344,c=433,则a ,b,c 大小关系是( )
A. b>c>a B. a>b>c C. c>a>b D. a<b<c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段 ![]() ,
, ![]() ,
, ![]() . 求作:矩形
. 求作:矩形 ![]() .
.
以下是甲、乙两同学的作业:
甲:① 以点 ![]() 为圆心,
为圆心, ![]() 长为半径作弧;
长为半径作弧;
② 以点 ![]() 为圆心,
为圆心, ![]() 长为半径作弧;
长为半径作弧;
③ 两弧在 ![]() 上方交于点
上方交于点 ![]() ,连接
,连接 ![]() ,
, ![]() .
.
四边形 ![]() 即为所求矩形.(如图)
即为所求矩形.(如图)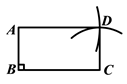
乙:① 连接 ![]() ,作线段
,作线段 ![]() 的垂直平分线,交
的垂直平分线,交 ![]() 于点
于点 ![]() ;
;
② 连接 ![]() 并延长,在延长线上取一点
并延长,在延长线上取一点 ![]() ,使
,使 ![]() ,连接
,连接 ![]() ,
, ![]() .
.
四边形 ![]() 即为所求矩形.(如图)
即为所求矩形.(如图)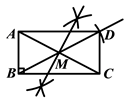
老师说甲、乙同学的作图都正确.
则甲的作图依据是:;
乙的作图依据是:.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() 的垂直平分线分别与
的垂直平分线分别与![]() ,
, ![]() 及
及![]() 的延长线相交于点
的延长线相交于点![]() ,
, ![]() ,
, ![]() ,且
,且![]() . ⊙O是
. ⊙O是![]() 的外接圆,
的外接圆, ![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交⊙O于点
,交⊙O于点![]() ,连接
,连接![]() ,
, ![]() .
.
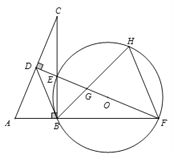
(1)求证: ![]() ;
;
(2)试判断![]() 与⊙O的位置关系,并说明理由;
与⊙O的位置关系,并说明理由;
(3)若![]() , 求
, 求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
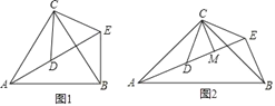
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
(1)证明:AD=BE;
(2)求∠AEB的度数.
问题变式:
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求出∠AEB的度数以及判断线段CM、AE、BE之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com