
【题目】问题探究:
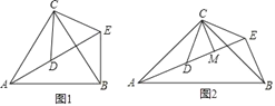
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
(1)证明:AD=BE;
(2)求∠AEB的度数.
问题变式:
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求出∠AEB的度数以及判断线段CM、AE、BE之间的数量关系,并说明理由.
【答案】探究展示:(1)证明见解析; (2)600.
拓展延伸:(1)∠AEB=900 ;(2)AE= 2CM+BE,理由见解析.
【解析】试题分析:问题探究:(1)先证出∠ACD=∠BCE,那么△ACD≌△BCE,根据全等三角形证出AD=BE;
(2)∠ADC=∠BEC,求出∠ADC=120°,得出∠BEC=120°,从而证出∠AEB=60°;
问题变式:证明△ACD≌△BCE,得出∠ADC=∠BEC、AD=BE,从而得到∠AEB的度数,再由等腰直角三角形的性质得到DM=ME=CM即可.
试题解析:问题探究:
(1) ∵△ACB和△DCE均为等边三角形,∴∠ACB=∠DCE=60°,AC=BC、DC=EC,∴∠ACD=∠BCE,∴△CDA≌△CEB, ∴AD=BE
(2)∵△CDA≌△CEB,∴∠CEB=∠CDA=1200,又∠CED=600,∴∠AEB=1200-600=600.
问题变式:
(1)∵△ACB和△DCE均为等腰直角三角形,∠ACB =∠DCE= 900,
∴AC=BC, CD=CE,
∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD= ∠BCE
∴△ACD≌△BCE
∴AD = BE, ∠BEC=∠ADC=1350.
∴∠AEB=∠BEC-∠CED=1350-450=900
(2)AE= 2CM+BE
在等腰直角三角形DCE中,CM为斜边DE上的高,
∴CM= DM= ME,∴DE=2CM.
∴AE=DE+AD=2CM+BE
∴AE= 2CM+BE


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】已知C为线段AB的中点,D为线段AC的中点.
(1)画出相应的图形,求出图中线段的条数并写出相应的线段;
(2)若图中所有线段的长度和为26,求线段AC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x,y为有理数,现规定一种运算“*”,满足x*y=xy+1(等式中xy表示x与y的积)
(1)求2*4的值;
(2)求(1*4)*(﹣2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚州市正在争创省文明城市,为了美化城市,改善人们的居住环境,我市深入开展绿化彩化美化工程,通过植草、种树、修建公园及树阵式停车位等多项措施,使城区绿地面积不断增加.请根据图中所提供的信息,回答下列问题: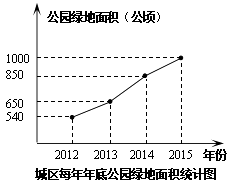
(1)2014年底的公园绿地面积为公顷,比2012年底增加了公顷;
(2)在2013年,2014年,2015年这三年中,绿地面积增加最多的是年;
(3)为满足城市发展的需要,计划到2017年底使城区公园绿地总面积达到1200公顷,试求2017年底公园绿地面积对2015年底的增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
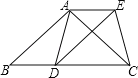
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:AD=CE;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→……,白甲壳虫爬行的路线是AB→BB1→……,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2015条棱分别停止在所到的正方体顶点处时,它们之间的距离是( ).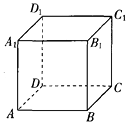
A.0 B.1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
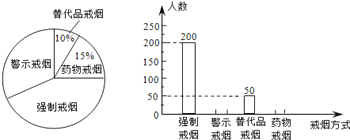
【题目】吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图:据统计图解答下列问题:
(1)同学们一共调查了多少人?
(2)将条形统计图补充完整。
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(4)为了让更多的市民增强“戒烟”意识,同学们在社区做了两期“警示戒烟”的宣传。若每期宣传后,市民支持“警示戒烟”的平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com