
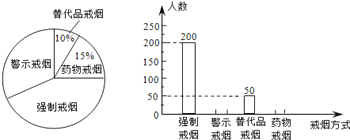
【题目】吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图:据统计图解答下列问题:
(1)同学们一共调查了多少人?
(2)将条形统计图补充完整。
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(4)为了让更多的市民增强“戒烟”意识,同学们在社区做了两期“警示戒烟”的宣传。若每期宣传后,市民支持“警示戒烟”的平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人?
【答案】(1)500人.(2)补图见解析;(3)3500人。(4)5040人.
【解析】试题分析:(1)根据替代品戒烟50人占总体的10%,即可求得总人数;
(2)根据求得的总人数,结合扇形统计图可以求得药物戒烟的人数,从而求得警示戒烟的人数,再根据各部分的人数除以总人数,即可求得各部分所占的百分比;
(3)根据图中“强制戒烟”的百分比再进一步根据样本估计总体.
(4)第一期宣传后支持“警示戒烟”的市民约有3500×(1+增长率),第二期宣传后支持“警示戒烟”的市民约有3500×(1+增长率)(1+增长率).
试题解析:(1)50÷10%=500(人).
故一共调查了500人.
(2)由(1)可知,总人数是500人.
药物戒烟:500×15%=75(人);
警示戒烟:500-200-50-75=175(人);175÷500=35%;
强制戒烟:200÷500=40%.
完整的统计图如图所示:
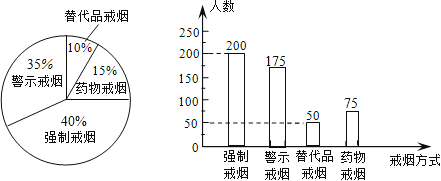
(3)10000×35%=3500(人),
答:大约有3500人支持“警示戒烟”这种方式;
(4)3500×(1+20%)2=5040(人),
答:两期宣传后支持“警示戒烟”的市民约有5040人.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】问题探究:
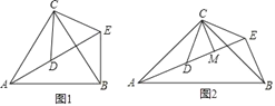
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
(1)证明:AD=BE;
(2)求∠AEB的度数.
问题变式:
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求出∠AEB的度数以及判断线段CM、AE、BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
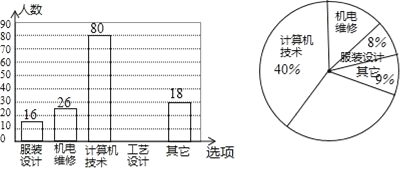
【题目】每年5月的第二周为:“职业教育活动周”,今年我市展开了以“弘扬工匠精神,打造技能强国”为主题的系列活动,活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动,相关职业技术人员进行了现场演示,活动后该校随机抽取了部分学生进行调查:“你最感兴趣的一种职业技能是什么?”并对此进行了统计,绘制了统计图(均不完整).
(1)补全条形统计图和扇形统计图;
(2)若该校共有3000名学生,请估计该校对“工艺设计”最感兴趣的学生有多少人?
(3)要从这些被调查的学生中随机抽取一人进行访谈,那么正好抽到对“机电维修”最感兴趣的学生的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
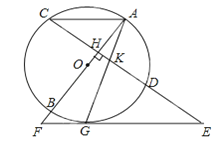
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于切点为G,连接AG交CD于K.
(1)求证:KE=GE;
(2)若KG2=KDGE,试判断AC与EF的位置关系,并说明理由;
(3)在(2)的条件下,若sinE=![]() ,AK=
,AK=![]() ,求FG的长.
,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,淮安动物园在7天假期中每天接待的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数),把9月30日的游客人数记为a万人.
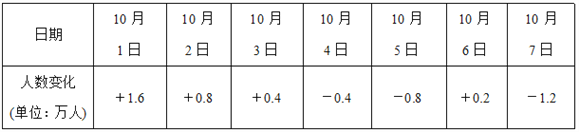
(1)请用含a的代数式表示10月2日的游客人数;
(2)请判断七天内游客人数最多的是哪天,有多少人?
(3)若9月30日的游客人数为2万人,门票每人10元,问黄金周期间淮安动物园门票收入是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com