
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于切点为G,连接AG交CD于K.
(1)求证:KE=GE;
(2)若KG2=KDGE,试判断AC与EF的位置关系,并说明理由;
(3)在(2)的条件下,若sinE=![]() ,AK=
,AK=![]() ,求FG的长.
,求FG的长.
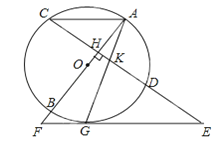
【答案】(1)证明见解析;(2)AC∥EF,证明见解析;(3)FG= ![]() .
.
【解析】试题分析:(1)如图1,连接OG.根据切线性质及CD⊥AB,可以推出∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE;
(2)AC与EF平行,理由为:如图2所示,连接GD,由∠KGE=∠GKE,及KG2=KDGE,利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似,又利用同弧所对的圆周角相等得到∠C=∠AGD,可推知∠E=∠C,从而得到AC∥EF;
(3)如图3所示,连接OG,OC,先求出KE=GE,再求出圆的半径,根据勾股定理与垂径定理可以求解;然后在Rt△OGF中,解直角三角形即可求得FG的长度.
试题解析:(1)如图1,连接OG.
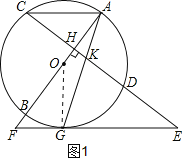
∵EG为切线,
∴∠KGE+∠OGA=90°,
∵CD⊥AB,
∴∠AKH+∠OAG=90°,
又∵OA=OG,
∴∠OGA=∠OAG,
∴∠KGE=∠AKH=∠GKE,
∴KE=GE.
(2)AC∥EF,理由为连接GD,如图2所示.
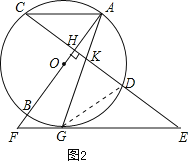
∵KG2=KDGE,即![]() ,
,
∴![]() ,
,
又∵∠KGE=∠GKE,
∴△GKD∽△EGK,
∴∠E=∠AGD,
又∵∠C=∠AGD,
∴∠E=∠C,
∴AC∥EF;
(3)连接OG,OC,如图3所示,
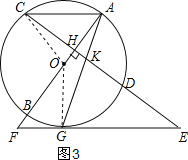
∵EG为切线,
∴∠KGE+∠OGA=90°,
∵CD⊥AB,
∴∠AKH+∠OAG=90°,
又∵OA=OG,
∴∠OGA=∠OAG,
∴∠KGE=∠AKH=∠GKE,
∴KE=GE.
∵sinE=sin∠ACH=![]()
,设AH=3t,则AC=5t,CH=4t,
∵KE=GE,AC∥EF,
∴CK=AC=5t,
∴HK=CK-CH=t.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,
即(3t)2+t2=(2![]() )2,解得t=
)2,解得t=![]() .
.
设⊙O半径为r,在Rt△OCH中,OC=r,OH=r-3t,CH=4t,
由勾股定理得:OH2+CH2=OC2,
即(r-3t)2+(4t)2=r2,解得r=![]() t=
t=![]() .
.
∵EF为切线,
∴△OGF为直角三角形,
在Rt△OGF中,OG=r=![]() ,tan∠OFG=tan∠CAH=
,tan∠OFG=tan∠CAH=![]() ,
,
∴FG=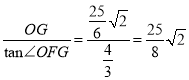


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→……,白甲壳虫爬行的路线是AB→BB1→……,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2015条棱分别停止在所到的正方体顶点处时,它们之间的距离是( ).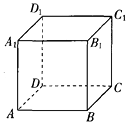
A.0 B.1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x , y)和Q(x , y′),给出如下定义:若 ![]() ,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2).
,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2).
结合定义,请回答下列问题: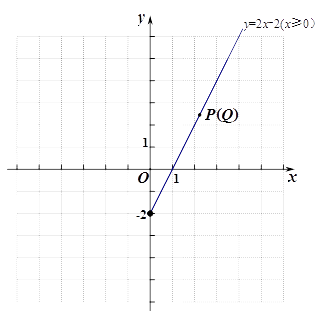
(1)点(-3,4)的“可控变点”为点 .
(2)若点N(m,2)是函数 ![]() 图象上点M的“可控变点”,则点M的坐标为;
图象上点M的“可控变点”,则点M的坐标为;
(3)点P为直线 ![]() 上的动点,当x≥0时,它的“可控变点”Q所形成的图象如下图所示(实线部分含实心点).请补全当x<0时,点P的“可控变点” Q所形成的图象;
上的动点,当x≥0时,它的“可控变点”Q所形成的图象如下图所示(实线部分含实心点).请补全当x<0时,点P的“可控变点” Q所形成的图象;
查看答案和解析>>
科目:初中数学 来源: 题型:
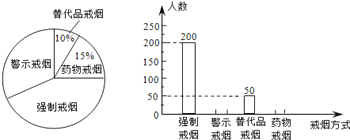
【题目】吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图:据统计图解答下列问题:
(1)同学们一共调查了多少人?
(2)将条形统计图补充完整。
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(4)为了让更多的市民增强“戒烟”意识,同学们在社区做了两期“警示戒烟”的宣传。若每期宣传后,市民支持“警示戒烟”的平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学实践探究活动中,大家遇到了这样的问题:
如图,在一个圆柱体形状的包装盒的底部A处有一只壁虎,在顶部B处有一只小昆虫,壁虎沿着什么路线爬行,才能以最短的路线接近小昆虫?
楠楠同学设计的方案是壁虎沿着A﹣C﹣B爬行;
浩浩同学设计的方案是将包装盒展开,在侧面展开图上连接AB,然后壁虎在包装盒的表面上沿着AB爬行.
在这两位同学的设计中,哪位同学的设计是最短路线呢?他们的理论依据是什么?( )
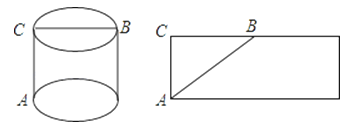
A. 楠楠同学正确,他的理论依据是“直线段最短”
B. 浩浩同学正确,他的理论依据是“两点确定一条直线”
C. 楠楠同学正确,他的理论依据是“垂线段最短”
D. 浩浩同学正确,他的理论依据是“两点之间,线段最短”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商人在一次买卖中均以120元卖出两件衣服,一件赚25%,一件赔25%,在这次交易中,该商人( )
A.赚16元
B.赔16元
C.不赚不赔
D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com