
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() 的垂直平分线分别与
的垂直平分线分别与![]() ,
, ![]() 及
及![]() 的延长线相交于点
的延长线相交于点![]() ,
, ![]() ,
, ![]() ,且
,且![]() . ⊙O是
. ⊙O是![]() 的外接圆,
的外接圆, ![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交⊙O于点
,交⊙O于点![]() ,连接
,连接![]() ,
, ![]() .
.
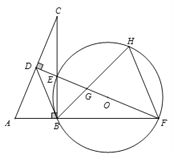
(1)求证: ![]() ;
;
(2)试判断![]() 与⊙O的位置关系,并说明理由;
与⊙O的位置关系,并说明理由;
(3)若![]() , 求
, 求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() 与
与![]() 相切. 理由见解析;(3)
相切. 理由见解析;(3)![]() .
.
【解析】试题分析:
(1)两个三角形都是直角三角形,有一条直角边相等,只需要得到另一组对应角相等即可;
(2)连接OB,设法结合(1)的结论得到∠DBC=∠OBC,证明∠DBO=90°;
(3)由△HFB与△HBF是一对相似三角形,得到![]() ,而△HEF是一个等腰直角三角形,则需要求EF的长,在直角△BEF中BE=AB=1,故要求BF的长,又BF=BC,BC=BE+CE,CE=AE,在直角△ABE中求得AE的长.
,而△HEF是一个等腰直角三角形,则需要求EF的长,在直角△BEF中BE=AB=1,故要求BF的长,又BF=BC,BC=BE+CE,CE=AE,在直角△ABE中求得AE的长.
试题解析:
(1)∵DF⊥AC,△ABC为Rt△,
∴∠CED=∠FEB, ![]() .
.
∠ABC=∠EBF=Rt∠,
又![]() ,∴
,∴![]() (
(![]() ).
).
(2)![]() 与
与![]() 相切. 理由如下:
相切. 理由如下:
连接![]() , ∵DF是AB的中垂线,∠ABC=90°,∴DB=DC=DA,
, ∵DF是AB的中垂线,∠ABC=90°,∴DB=DC=DA,
∴∠DBC=∠C.
由(1)∠DCB=∠EFB,而∠EFB=∠OBF,∴∠DBC=∠OBF.
∴![]() ,
,
∴![]() .∴BD与⊙O相切.
.∴BD与⊙O相切.
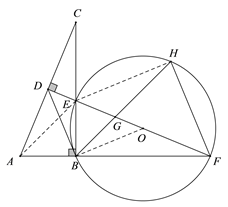
(3)连接![]() ,AE.
,AE.
∵BH是∠EBF的平分线,∴∠EBH=∠HBF=45°. ∠HFE=∠HBE=45°.
又∠GHF=∠FHB,∴△GHF∽△FHB,
∴![]() =
=![]() ,∴HG·HB=HF2.
,∴HG·HB=HF2.
∵⊙O是Rt△BEF的外接圆,∴EF为⊙O的直径,∴∠EHF=90°,
又∠HFE=45°,∴EH=HF. ∴EF2=EH2
∵DF是线段AC的垂直平分线,∴AE=CE,
又∵![]() ,∴AB=BE=1,∴AE=CE=
,∴AB=BE=1,∴AE=CE=![]() ,所以BF=BC=
,所以BF=BC=![]() ,
,
由勾股定理得, ![]() ,
,
∴![]() ,∴
,∴![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图![]()
(1)填空:AB= , BC=;
(2)若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动.试探索:BC﹣AB的值是否随着时间的变化而改变?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知C为线段AB的中点,D为线段AC的中点.
(1)画出相应的图形,求出图中线段的条数并写出相应的线段;
(2)若图中所有线段的长度和为26,求线段AC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=58°,OD平分∠AOC,∠DOE=90°.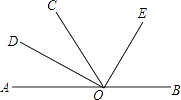
(1)求出∠BOD的度数;
(2)请通过计算说明:OE是否平分∠BOC.
查看答案和解析>>
科目:初中数学 来源: 题型:
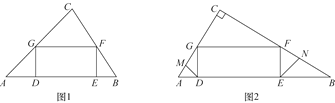
【题目】在面积为24的△ABC中,矩形DEFG的边DE在AB上运动,点F,G分别在边BC,AC上.
(1)若AB=8,DE=2EF,求GF的长;
(2)若![]() ,如图2,线段DM,EN分别为△ADG和△BEF的角平分线,求证:MG=NF;
,如图2,线段DM,EN分别为△ADG和△BEF的角平分线,求证:MG=NF;
(3)求出矩形DEFG的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→……,白甲壳虫爬行的路线是AB→BB1→……,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2015条棱分别停止在所到的正方体顶点处时,它们之间的距离是( ).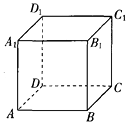
A.0 B.1 C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com