
【题目】如图,O为直线AB上一点,∠AOC=58°,OD平分∠AOC,∠DOE=90°.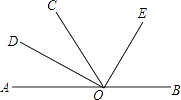
(1)求出∠BOD的度数;
(2)请通过计算说明:OE是否平分∠BOC.
【答案】
(1)解:∵∠AOC=58°,OD平分∠AOC,
∴∠AOD=29°,
∴∠BOD=180°﹣29°=151°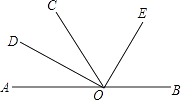
(2)解:OE是∠BOC的平分线.理由如下:
∵∠AOC=58°,
∴∠BOC=122°.
∵OD平分∠AOC,
∴∠DOC= ![]() ×58°=29°.
×58°=29°.
∵∠DOE=90°,
∴∠COE=90°﹣29°=61°,
∴∠COE= ![]() ∠BOC,即OE是∠BOC的平分线
∠BOC,即OE是∠BOC的平分线
【解析】(1)根据角平分线的定义得出∠AOD=29°,根据邻补角的定义得出∠BOD=180°﹣29°=151° ;
(2)OE是∠BOC的平分线.理由如下:根据邻补角的定义得出∠BOC=122°.根据角平分线的定义得出∠DOC= ![]() ×58°=29°.根据角的和差得出∠COE=90°﹣29°=61°,从而得出结论。
×58°=29°.根据角的和差得出∠COE=90°﹣29°=61°,从而得出结论。
【考点精析】关于本题考查的角的平分线和角的运算,需要了解从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】下列命题中,不一定成立的是( )
A.圆既是中心对称图形又是轴对称图形
B.弦的垂线经过圆心且平分这条弦所对的弧
C.弧的中点与圆心的连线垂直平分这条弧所对的弦
D.垂直平分弦的直线必过圆心
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】剪纸是中国古老的汉族传统民间艺术之一.下面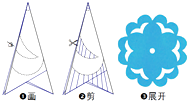
是制作剪纸的简单流程,展开后的剪纸图案从对称性来判断( )
A.是轴对称图形但不是中心对称图形
B.是中心对称图形但不是轴对称图形
C.既是轴对称图形也是中心对称图形
D.既不是轴对称图形也不是中心对称图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段 ![]() ,
, ![]() ,
, ![]() . 求作:矩形
. 求作:矩形 ![]() .
.
以下是甲、乙两同学的作业:
甲:① 以点 ![]() 为圆心,
为圆心, ![]() 长为半径作弧;
长为半径作弧;
② 以点 ![]() 为圆心,
为圆心, ![]() 长为半径作弧;
长为半径作弧;
③ 两弧在 ![]() 上方交于点
上方交于点 ![]() ,连接
,连接 ![]() ,
, ![]() .
.
四边形 ![]() 即为所求矩形.(如图)
即为所求矩形.(如图)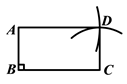
乙:① 连接 ![]() ,作线段
,作线段 ![]() 的垂直平分线,交
的垂直平分线,交 ![]() 于点
于点 ![]() ;
;
② 连接 ![]() 并延长,在延长线上取一点
并延长,在延长线上取一点 ![]() ,使
,使 ![]() ,连接
,连接 ![]() ,
, ![]() .
.
四边形 ![]() 即为所求矩形.(如图)
即为所求矩形.(如图)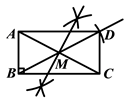
老师说甲、乙同学的作图都正确.
则甲的作图依据是:;
乙的作图依据是:.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,将直线l1:y=﹣2x﹣1平移后,得到直线l2:y=﹣2x+5,则下列平移作法正确的是( )
A.将l1向右平移3个单位B.将l1向右平移6个单位
C.将l1向左平移3个单位D.将l1向左平移6个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() 的垂直平分线分别与
的垂直平分线分别与![]() ,
, ![]() 及
及![]() 的延长线相交于点
的延长线相交于点![]() ,
, ![]() ,
, ![]() ,且
,且![]() . ⊙O是
. ⊙O是![]() 的外接圆,
的外接圆, ![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交⊙O于点
,交⊙O于点![]() ,连接
,连接![]() ,
, ![]() .
.
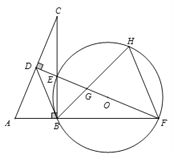
(1)求证: ![]() ;
;
(2)试判断![]() 与⊙O的位置关系,并说明理由;
与⊙O的位置关系,并说明理由;
(3)若![]() , 求
, 求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在9×7的小正方形网格中,△ABC的顶点A,B,C在网格的格点上.将△ABC向左平移3个单位、再向上平移3个单位得到△A′B′C′.再将△ABC按一定规律依次旋转:第1次,将△ABC绕点B顺时针旋转![]() 得到△
得到△![]() ;第2次,将△
;第2次,将△![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到△
得到△![]() ;第3次,将△
;第3次,将△![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到△
得到△![]() ;第4次,将△
;第4次,将△![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到△
得到△![]() 依次旋转下去.
依次旋转下去.

(1)在网格中画出△A′B′C′和△![]() ;
;
(2)请直接写出至少在第几次旋转后所得的三角形刚好为△A′B′C′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(x﹣1)2﹣4的图象先向左平移2个单位,再向上平移3个单位,所得函数解析式为( )
A.y=(x﹣1)2+1
B.y=(x﹣3)2﹣1
C.y=(x+1)2﹣1
D.y=(x+2)2+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级一班开展了一次“纪念抗日战争胜利七十周年”知识竞赛,竞赛题一共有20道题,下表是其中四位参赛选手的答对题数和不答或答错题数及得分情况,请你根据表格中所给的信息回答下列问题: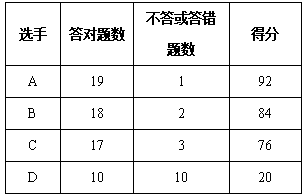
(1)问答对一题得多少分,不答或答错一题扣多少分?
(2)一位同学说他得了75分,请问可能吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com