
ЁОЬтФПЁПвбжЊЃКЁЯMON=80ЁуЃЌOEЦНЗжЁЯMONЃЌЕуAЁЂBЁЂCЗжБ№ЪЧЩфЯпOMЁЂOEЁЂONЩЯЕФЖЏЕуЃЈAЁЂBЁЂCВЛгыЕуO жиКЯЃЉЃЌСЌНгACНЛЩфЯпOEгкЕуDЃЎЩшЁЯOAC=xЁуЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєABЁЮONЃЌдђЃКЂйЁЯABOЕФЖШЪ§ЪЧЁЁЁЁЁЁЁЁЁЁЁЁЃЛ
ЂкШчЭМ2ЃЌЕБЁЯBAD=ЁЯABDЪБЃЌЪдЧѓxЕФжЕЃЈвЊЫЕУїРэгЩЃЉЃЛ
ЃЈ2ЃЉШчЭМ3ЃЌШєABЁЭOMЃЌдђЪЧЗёДцдкетбљЕФXЕФжЕЃЌЪЙЕУЁїADBжагаСНИіЯрЕШЕФНЧЃПШєДцдкЃЌжБНгаДГіxЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎЃЈздМКЛЭМЃЉ

ЁОД№АИЁПЃЈ1ЃЉЂйЁЯABOЕФЖШЪ§400Ђкx=600ЃЈ2ЃЉДцдкетбљЕФxЃЌx=100Лђx=250Лђx=400
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЂйИљОнЬѕМўЁЯMON=80ЁуЃЌOEЦНЗжЁЯMONЃЌПЩЕУЁЯAOB=ЁЯNOB =40ЁуЃЌдйИљОнABЁЮONЃЌЕУЁЯABO=ЁЯNOB =40Ёу;ЂкИљОнЂйЕФНсТлНсКЯЬѕМўЁЯBAD=ЁЯABD ПЩЧѓГіЁЯ2=400ЃЌЁЯ4=800ЃЌдйИљОнШ§НЧаЮЕФФкНЧКЭПЩЧѓГіx=600ЃЈ2ЃЉЗжЕБЕуDдкЯпЖЮOBЩЯЪБКЭ ЕБЕуDдкЩфЯпBEЩЯЪБ,СНжжЧщПіЬжТлЃКДцдкетбљЕФxЃЌx=10ЁуЛђx=25ЁуЛђx=40Ёу
ЪдЬтНтЮіЃКЃЈ1ЃЉ
ЂйЁЯABOЕФЖШЪ§ЪЧ40Ёу
ЂкЁпЁЯMON=80ЁуЃЌЧвOEЦНЗжЁЯMONЃЌЁрЁЯ1=ЁЯ2=40ЁуЃЌ
гжЁпAB//ONЃЌЁрЁЯ3=ЁЯ1=40Ёу
ЁпЁЯBAD=ЁЯABDЃЌЁрЁЯBAD=40ЁуЃЌ
ЁрЁЯ4=80ЁуЃЌ
ЁрЁЯOAC=600ЃЌМДx=60Ёу
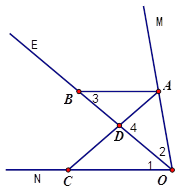
ЃЈ2ЃЉЃЈБОаЁЬт4ЗжЃЌУПИі1ЗжЃЌШЋЖд4ЗжЃЉ
ДцдкетбљЕФxЃЌ
x=10Ёу
x=25Ёу
x=40Ёу


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдке§ЗНаЮABCDжаЃЌEЪЧABЩЯвЛЕуЃЌFЪЧADбгГЄЯпЩЯвЛЕуЃЌЧвDF=BEЃЎ
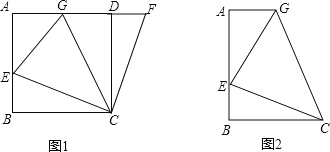
ЃЈ1ЃЉЂйЪдЫЕУїCE=CFЃЌЁЯBCE=ЁЯDCFЃЛ
ЂкШчЭМ1ЃЌШєЕуGдкADЩЯЃЌЧвЁЯGCE=45ЁуЃЌдђGE=GFГЩСЂТ№ЃПЮЊЪВУДЃП
ЃЈ2ЃЉдЫгУЃЈ1ЃЉжаЛ§РлЕФОбщКЭжЊЪЖЃЌЭъГЩЯТЬтЃК
ШчЭМ2ЃЌдкЬнаЮABCGжаЃЌAGЁЮBCЃЌBCЃОAGЃЌЁЯB=90ЁуЃЌAB=BC=6ЃЌEЪЧABЩЯ вЛЕуЃЌЧвЁЯGCE=45ЁуЃЌBE=2ЃЌЧѓGEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћ5x+3гыЃ2x+9ЪЧЛЅЮЊЯрЗДЪ§ЃЌдђxЕФжЕЪЧ_______
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЗжНтвђЪНЃК
ЃЈ1ЃЉ2x2Љ8ЃЛ
ЃЈ2ЃЉЉ3ax2+6axyЉ3ay2 ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћЯђЖЋзп6УзМЧзї+6УзЃЌФЧУДЯђЮїзп10УзМЧзї_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЁЮFCЃЌDЪЧABЩЯвЛЕуЃЌDFНЛACгкЕуEЃЌDE=FEЃЌЗжБ№бгГЄFDКЭCBНЛгкЕуGЃЎ
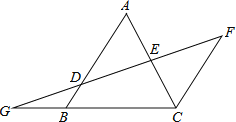
ЃЈ1ЃЉЧѓжЄЃКЁїADEЁеЁїCFEЃЛ
ЃЈ2ЃЉШєGB=2ЃЌBC=4ЃЌBD=1ЃЌЧѓABЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫФИібЁЯюжаЃЌВЛЪЧyЙигкxЕФКЏЪ§ЕФЪЧЃЈ ЃЉ
AЃЎ|y|=xЉ1 BЃЎy=![]() CЃЎy=2xЉ7 DЃЎy=x2
CЃЎy=2xЉ7 DЃЎy=x2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгРМЮЯиФГЗЇУХЙЋЫОгУAаЭКЭBаЭИжАхжЦзїCаЭКЭDаЭСуМў. вбжЊ1ПщAаЭИжАхПЩжЦзїГЩ3ПщCаЭСуМўКЭ2ПщDаЭСуМўЃЛгУ1ПщBаЭИжАхПЩжЦзїГЩ1ПщCаЭСуМўКЭ3ПщDаЭСуМў.
ЃЈ1ЃЉ гУ2ПщAаЭКЭ3ПщBаЭИжАхЃЌПЩжЦзїГЩCаЭСуМў ПщЃЌ DаЭСуМў Пщ.
ЃЈ2ЃЉШєвЊжЦзї35ПщCаЭСуМўЃЌ28ПщDаЭСуМўЃЌашвЊгУAаЭКЭBаЭИжАхИїЖрЩйПщЃП
ЃЈ3ЃЉ ЯжашCЃЌDСНжжаЭКХЕФСуМўЙВ67ПщЃЌашвЊгУA, BСНжжИжАхИїЖрЩйПщЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com