
【题目】如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
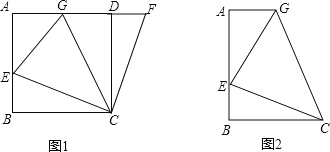
(1)①试说明CE=CF,∠BCE=∠DCF;
②如图1,若点G在AD上,且∠GCE=45°,则GE=GF成立吗?为什么?
(2)运用(1)中积累的经验和知识,完成下题:
如图2,在梯形ABCG中,AG∥BC,BC>AG,∠B=90°,AB=BC=6,E是AB上 一点,且∠GCE=45°,BE=2,求GE的长.
【答案】(1)成立(2)GE=5
【解析】
试题分析:(1)①根据正方形的性质可得BC=CD,再利用“边角边”证明△BCE和△DCF全等,根据全等三角形对应边相等、对应角相等的单结论;
②根据全等三角形对应角相等可得∠BCE=∠DCF,再求出∠GCF=45°,从而得到∠GCF=∠GCE,再利用“边角边”证明△GCE和△GCF全等,根据全等三角形对应边相等可得EG=GF;
(2)设EG=x,根据(1)的结论表示出AG,再求出AE,然后在Rt△AEG中,利用勾股定理列出方程求解即可.
(1)①证明:在正方形ABCD中,BC=CD,
在△BCE和△DCF中,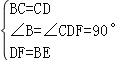 ,
,
∴△BCE≌△DCF(SAS),
∴CE=CF;,∠BCE=∠DCF
②EG=BE+GD.
理由如下:∵△BCE≌△DCF,
∴∠BCE=∠DCF,
∵∠GCE=45°,
∴∠GCF=∠GCD+∠DCF=∠GCD+∠BCE=90°﹣45°=45°,
∴∠GCF=∠GCE,
在△GCE和△GCF中,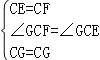 ,
,
∴△GCE≌△GCF(SAS),
∴EG=GF;
(2)设EG=x,
由(1)可知,BE+(6﹣AG)=EG,
即2+(6﹣AG)=x,
∴AG=8﹣x,
又∵AE=AB﹣BE=6﹣2=4,
∴在Rt△AEG中,AE2+AG2=EG2,
即42+(8﹣x)2=x2,
解得x=5,
即GE=5.


科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 与一次函数y2=kx+b的图象交于两点A(n,﹣1)、B(1,2).
与一次函数y2=kx+b的图象交于两点A(n,﹣1)、B(1,2).
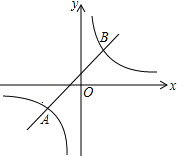
(1)求反比例函数与一次函数的关系式;
(2)根据图象,直接回答:当x取何值时,y1≥y2?
(3)连接OA、OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=200°,则∠P=( )

A. 10 ° B .20 ° C .30° D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.

(1)求证:△ACE≌△DBF;
(2)如果把△DBF沿AD折翻折使点F落在点G,连接BE和CG. 求证:四边形BGCE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,商业大厦推出全场打八折的优惠活动,持贵宾卡可在八折基础上继续打折,小明妈妈持贵宾卡买了标价为1000元的商品,共节省280元,则用贵宾卡又享受了______折优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的X的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com