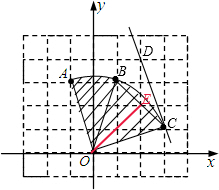
解:(1)如图所示,点B为所求的点,坐标为(1,3);
(2)作出图形,如图所示;
由勾股定理得:OA=

,
则弧AC长为

=

π;
(3)作出弧AC的切线CD,找出D坐标为(2,4),
由图形得到直线AD为减函数,即y随x的增大而减小;
(4)作OE⊥BC,
∵OB=OC,
∴OE为∠BOC的平分线,
∴∠BOE=∠COE=

∠BOC,
∵∠BCD=

∠BOC,
∴∠BCD=∠COE,
在Rt△OCE中,CE=

,OE=2

,
则tan∠BCD=tan∠COE=
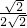
=

.
故答案为:(1)1;3;(2)

π;(3)减小;(4)

分析:(1)作出A关于y轴的对称点B,写出B坐标即可;
(2)根据题意作出线段OA扫过的平面区域,如图所示,弧AC的圆心角为直角,求出半径OA的长,利用弧长公式就求出弧AC长;
(3)作出弧AC的切线CD,根据网格找出D点,由直线CD的位置判断出直线CD为减函数,即可得到结果;
(4)过O作OE垂直于BC,由OB=OC,得到OE为角平分线,利用弦切角等于夹弧所对的圆周角,及角平分线定义得到∠BCD=∠COE,在直角三角形OCE中,由CE与OE长,利用锐角哦三角函数定义求出tan∠COE的值,即为tan∠BCD的值.
点评:此题考查了作图-旋转变换,锐角三角函数定义,勾股定理,弧长的计算,圆周角定理,以及切线的性质,作出正确的图形是解本题的关键.

 如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).
如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3). 解:(1)如图所示,点B为所求的点,坐标为(1,3);
解:(1)如图所示,点B为所求的点,坐标为(1,3); ,
, =
= π;
π; ∠BOC,
∠BOC, ∠BOC,
∠BOC, ,OE=2
,OE=2 ,
,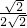 =
= .
. π;(3)减小;(4)
π;(3)减小;(4)


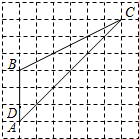 如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE=
如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE=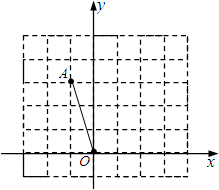 如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).
如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).