
 ��ͼ����֪�ڳ�����ABCD�У�AD=10��CD=5����E�ӵ�D���������߶�DA��ÿ��1����λ�����ٶ����A�����ƶ���ͬʱ��F�ӵ�C������������CD������ÿ��2����λ�����ٶ��ƶ�����B��E��F���㹲��ʱ������ͬʱֹͣ�˶�����ʱBF��CE�����E�ƶ���ʱ��Ϊt���룩��
��ͼ����֪�ڳ�����ABCD�У�AD=10��CD=5����E�ӵ�D���������߶�DA��ÿ��1����λ�����ٶ����A�����ƶ���ͬʱ��F�ӵ�C������������CD������ÿ��2����λ�����ٶ��ƶ�����B��E��F���㹲��ʱ������ͬʱֹͣ�˶�����ʱBF��CE�����E�ƶ���ʱ��Ϊt���룩������ ��1�������˶��ص��ʾ���߶Σ����ɹ��ɶ������ɣ�
��2���ɹ��ɶ������㼴�ɣ�
��3���ɾ��ε����ʣ���AD��BC����EC�ǡ�BED��ƽ���ߣ��жϳ�BE=BC���ɣ�
��4����EFC�ǵ���������ʱ��������������ۣ���E��C��F�ֱ�Ϊ���㣩�������̼��ɣ�
��� �⣺��1��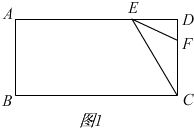
��0��t��2.5ʱ����ͼ1��
�ڳ�����ABCD�У�AD=10��CD=5��
���ADC=90��
����������DE=t��FC=5-2t��
��DF=5-2t��
���ݹ��ɶ����ã�EF2=DE2+DF2��CE2=DE2+CD2
��EF=$\sqrt{{t}^{2}+��5-2t��^{2}}$��CE=$\sqrt{{t}^{2}+25}$��
��2.5��t��5ʱ����ͼ2��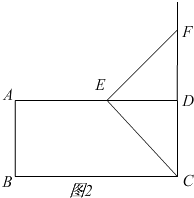
����������DE=t��FC=2t-5��
��EF=$\sqrt{{t}^{2}+��5-2t��^{2}}$��CE=$\sqrt{{t}^{2}+25}$��
��2������ͬʱֹͣ�˶�������BF��CE����ͼ3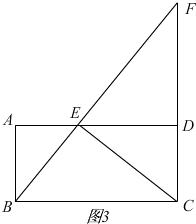
��Rt��FEC����EF2+EC2=FC2��
��t2+��2t-5��2+t2+52=��2t��2��
��t=5��
��3����EC�ǡ�BED��ƽ����ʱ��
���BEC=��DEC��
�ڳ�����ABCD�У�AD��BC��
���DEC=��BCE��
���BEC=��BCE��
��BE=BC��
��Rt��ABE��AB2+AE2=BE2��
��25+��10-t��2=100��
��t=10-5$\sqrt{3}$��t=10+5$\sqrt{3}$���ᣩ��
��t=10-5$\sqrt{3}$��
��4������EFC�ǵ���������ʱ��
��E�Ƕ��㣬
��CE=EF��
��$\sqrt{{t}^{2}+��5-2t��^{2}}$=$\sqrt{{t}^{2}+25}$��
��t=5��t=0���ᣩ
��CΪ����ʱ
��CE=CF��
��$\sqrt{{t}^{2}+25}$=2t��
��t=$\frac{5\sqrt{3}}{3}$��t=-$\frac{5\sqrt{3}}{3}$���ᣩ��
��FΪ����ʱ��
��EF=CF��
��$\sqrt{{t}^{2}+��5-2t��^{2}}$=2t
��t=10-5$\sqrt{3}$ ��t=10+5$\sqrt{3}$���ᣩ
��EFC�ǵ���������ʱ��t=5��t=$\frac{5\sqrt{3}}{3}$��t=10-5$\sqrt{3}$��
���� �������ı����ۺ��⣬��Ҫ�����˾��ε����ʣ���ƽ���ߵ����壬���������ε����ʣ����˶�ʱ��t��ʾ�߶��ǽⱾ��Ĺؼ����������⻭��ͼ���DZ�����ѵ㣮


 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��3 | B�� | 3��4 | C�� | 4��5 | D�� | 5��6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
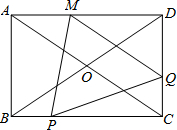 ��ͼ������ABCD�У��Խ���AC��BD���ڵ�O��AB=6��BC=8������P�ӵ�B������BC������ÿ��1����λ���ȵ��ٶ����C�����˶���ͬʱ����Q�ӵ�C������CD������ÿ��1����λ���ȵ��ٶ����D�����˶���������һ���㵽���յ��ֹͣ�˶�������Q��QM��AC��AD�ڵ�M������PM��PQ�����P���˶�ʱ��Ϊt�룬��PQM�����Ϊs��
��ͼ������ABCD�У��Խ���AC��BD���ڵ�O��AB=6��BC=8������P�ӵ�B������BC������ÿ��1����λ���ȵ��ٶ����C�����˶���ͬʱ����Q�ӵ�C������CD������ÿ��1����λ���ȵ��ٶ����D�����˶���������һ���㵽���յ��ֹͣ�˶�������Q��QM��AC��AD�ڵ�M������PM��PQ�����P���˶�ʱ��Ϊt�룬��PQM�����Ϊs���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{24}$ | B�� | $\sqrt{5}$ | C�� | $\sqrt{12}$ | D�� | $\sqrt{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
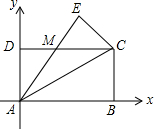 ��ͼ����ƽ��ֱ������ϵ�У���һ����ABCD������A��0��0����B��m��0����D��0��n����m����ӽ�$\sqrt{65}$��������n��16������ƽ������������ABC�ؾ��ζԽ���AC����ֱ�߷��ۣ���B���ڵ�E����AE���CD�ཻ�ڵ�M��
��ͼ����ƽ��ֱ������ϵ�У���һ����ABCD������A��0��0����B��m��0����D��0��n����m����ӽ�$\sqrt{65}$��������n��16������ƽ������������ABC�ؾ��ζԽ���AC����ֱ�߷��ۣ���B���ڵ�E����AE���CD�ཻ�ڵ�M���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ������һЩ��ͬ��С��������ɵļ����������ͼ����ͼ�����������������С������ĸ���Ϊn����n�����ֵΪ��������
��ͼ��ʾ������һЩ��ͬ��С��������ɵļ����������ͼ����ͼ�����������������С������ĸ���Ϊn����n�����ֵΪ��������| A�� | 8 | B�� | 9 | C�� | 10 | D�� | 11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ɽ��ʡ���������ص���Э�������꼶3��ѧҵˮƽģ�⿼����ѧ�Ծ��������棩 ���ͣ���ѡ��
�����ĸ�ͼ���У���Գ�ͼ���У�������
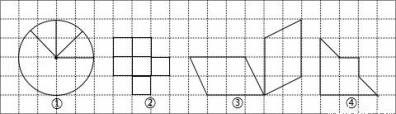
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com