练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

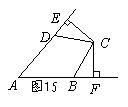
    如图15，点D、B分别在∠A的两边上，C是∠A内一点，且AB=AD，BC=DC，CE⊥AD，CF⊥AB，垂足分别为E、F，求证：CE=CF。

     


    证明：连结AC，则△ADC≌△ABC，

    ∴∠DAC=∠BAC，又∵CE⊥AD，CF⊥AB，∴CE=CF.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

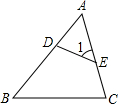    精英家教网如图所示，D，E分别是△ABC的边AB、AC上的点，∠1=∠B，AE=EC=4，BC=10，AB=12，则△ADE和△ABC的周长之比为（　　）
    A、
    1
    2
    B、
    1
    3
    C、
    1
    4
    D、
    1
    5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    问题情境：如图1，在直角三角形ABC中，∠BAC=90°，AD⊥BC于点D，可知：∠BAD=∠C（不需要证明）；
    特例探究：如图2，∠MAN=90°，射线AE在这个角的内部，点B、C在∠MAN的边AM、AN上，且AB=AC，CF⊥AE于点F，BD⊥AE于点D．证明：△ABD≌△CAF；
    归纳证明：如图3，点B，C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，∠1=∠2=∠BAC．求证：△ABE≌△CAF；
    拓展应用：如图4，在△ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为15，则△ACF与△BDE的面积之和为
    5
    5
    ．

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年上海市松江区九年级下学期3月月考数学试卷（解析版） 题型：解答题

    （本题满分14分，其中第（1）题4分，第（2）题的第?、?小题分别为4分、6分）

    如图1，在△ABC中，已知AB=15，cosB=，tanC=．点D为边BC上的动点（点D不与B、C重合），以D为圆心，BD为半径的⊙D交边AB于点E．

    （1）设BD=x，AE=y，求与的函数关系式，并写出函数定域义；

    （2）如图2，点F为边AC上的动点，且满足BD=CF，联结DF．

    ①当△ABC和△FDC相似时，求⊙D的半径；

    ② 当⊙D与以点F为圆心，FC为半径⊙F外切时，求⊙D的半径．

     

    查看答案和解析>>

    科目：初中数学 来源：2009年初中毕业升学考试（辽宁大连卷）数学（解析版） 题型：解答题

    如图15，在△ABC和△PQD中，AC = k BC，DP = k DQ，∠C =∠PDQ，D、E分别是AB、AC的中点，点P在直线BC上，连结EQ交PC于点H．猜想线段EH与AC的数量关系，并证明你的猜想．

     

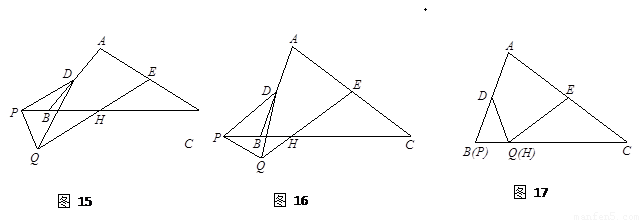
    查看答案和解析>>

    科目：初中数学 来源：2014届江苏省初一上学期期末数学试卷（解析版） 题型：填空题

     

    1.已知：如图7，点C在线段AB上，线段AC=15，BC=5，点M、N分别是AC、BC的中点，求MN的长度．

    2.根据（1）的计算过程与结果，设AC+BC=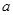，其它条件不变，你能猜出MN的长度吗？请用简洁的语言表达你发现的规律．

    3.若把（1）中的“点C在线段AB上”改为“点C在直线AB上”，其它条件不变，结论又如何？请说明你的理由．

     

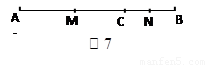
    查看答案和解析>>

    同步练习册答案