
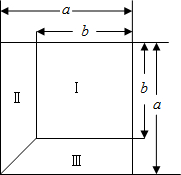
 根据图示,回答下列问题
根据图示,回答下列问题分析 (1)根据正方形的面积即可得出结论;
(2)先求出梯形的底和高,再由梯形的面积公式即可得出结论;
(3)求出SI的值,再比较SⅡ+SⅢ与S-SⅠ的值即可;
(4)根据(3)的结果可得出结论.
解答 解:(1)∵大由图可知正方形的边长为a,
∴S=a2;
(2)∵梯形Ⅱ的上底是b,下底是a,高是a-b,
∴SⅡ=$\frac{1}{2}$(a+b)(a-b)=$\frac{1}{2}$(a2-b2).
同理,梯形Ⅲ的上底是b,下底是a,高是a-b
SⅢ=$\frac{1}{2}$(a+b)(a-b)=$\frac{1}{2}$(a2-b2);
(3)∵S=a2,SI=b2,SⅡ=SⅢ=$\frac{1}{2}$(a+b)(a-b)=$\frac{1}{2}$(a2-b2),
∴SⅡ+SⅢ=a2-b2,S-SⅠ=a2-b2;
(4)根据(3)得:SⅡ+SⅢ=S-SⅠ=a2-b2.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
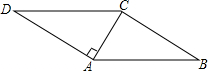 在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是( )
在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是( )| A. | 4+2$\sqrt{3}$ | B. | 8 | C. | 8+4$\sqrt{3}$ | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
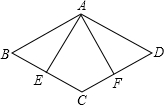 在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,则∠EAF等于( )
在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E、F分别为BC、CD的中点,则∠EAF等于( )| A. | 60° | B. | 55° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
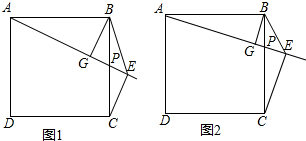
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ab$\sqrt{ab}$ | B. | -ab$\sqrt{b}$ | C. | ab$\sqrt{b}$ | D. | ab2$\sqrt{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com