练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一辆慢车和一辆快车沿相同的路线从A地到B地，所行驶的路程与时间的函数图形如图所示，下列说法正确的有（ ）

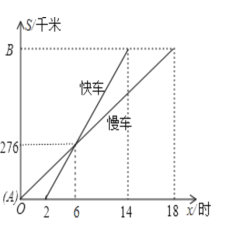
    ①快车追上慢车需6小时；②慢车比快车早出发2小时；③快车速度为46km/h；④慢车速度为46km/h； ⑤A、B两地相距828km；⑥快车从A地出发到B地用了14小时

    A. 2个B. 3个C. 4个D. 5个

    【答案】B

    【解析】

    根据图形给出的信息求出两车的出发时间，速度等即可解答．

    解：①两车在276km处相遇，此时快车行驶了4个小时，故错误．

    ②慢车0时出发，快车2时出发，故正确．

    ③快车4个小时走了276km，可求出速度为69km/h，错误．

    ④慢车6个小时走了276km，可求出速度为46km/h，正确．

    ⑤慢车走了18个小时，速度为46km/h，可得A,B距离为828km，正确．

    ⑥快车2时出发，14时到达，用了12小时，错误．

    故答案选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】学习过绝对值之后，我们知道:|5－2|表示 5 与 2 的差的绝对值，实际上也可理解为 5 与 2 两数在数轴上所对应的两点之间的距离：|5+2|表示 5 与－2 的差的绝对值，实际上也可理解为 5 与－2 两数在数轴上所对应的两点之间的距离. 试探究解决以下问题：

    ⑴|x+6|可以理解为 与 两数在数轴上所对应的两点之间的距离；

    ⑵找出所有符合条件的整数 x，使|x+1|+|x－2|=3 成立；

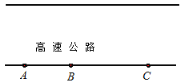
    ⑶如图，在一条笔直的高速公路旁边依次有 A、B、C 三个城市，它们距高速公路起点的距离分别是 567km、689km、889km.现在需要在该公路旁建一个物流集散中心 P，请直接指出该物流集散中心 P 应该建设在何处，才能使得 P 到三个城市的距离之和最小?这个最小距离是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市举行“传承好家风”征文比赛，已知每篇参赛征文成绩记m分（60≤m≤100），组委会从1000篇征文中随机抽取了部分参赛征文，统计了他们的成绩，并绘制了如下不完整的两幅统计图表.

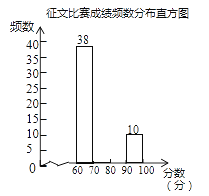
    请根据以上信息，解决下列问题：

    （1）征文比赛成绩频数分布表中c的值是________；

    （2）补全征文比赛成绩频数分布直方图；

    （3）若80分以上（含80分）的征文将被评为一等奖，试估计全市获得一等奖征文的篇数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

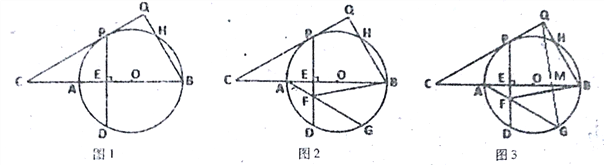
    【题目】已知：如图，AB为⊙O的直径，C是BA延长线上一点，CP切⊙O于P，弦PD⊥AB于E，过点B作BQ⊥CP于Q，交⊙O于H．

    （1）如图1，求证：PQ=PE；

    （2）如图2，G是圆上一点，∠GAB=30，连接AG交PD于F，连接BF，tan∠BFE=，求∠C的度数；

    （3）如图3，在（2）的条件下，PD=6，连接QG交BC于点M，求QM的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F，若BF=12，AB=10，则AE的长为（　　）

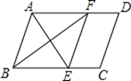
    A. 13B. 14C. 15D. 16

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，CD是边AB上的中线，∠B是锐角，且sinB=，tanA=，BC=2，求边AB的长和cos∠CDB的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“幸福是奋斗出来的”，在数轴上，若C到A的距离刚好是3，则C点叫做A的“幸福点”，若C到A、B的距离之和为6，则C叫做A、B的“幸福中心”

    （1）如图1，点A表示的数为﹣1，则A的幸福点C所表示的数应该是　 　；

    （2）如图2，M、N为数轴上两点，点M所表示的数为4，点N所表示的数为﹣2，点C就是M、N的幸福中心，则C所表示的数可以是　 　（填一个即可）；

    （3）如图3，A、B、P为数轴上三点，点A所表示的数为﹣1，点B所表示的数为4，点P所表示的数为8，现有一只电子蚂蚁从点P出发，以2个单位每秒的速度向左运动，当经过多少秒时，电子蚂蚁是A和B的幸福中心？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学是一门充满乐趣的学科，某校七年级小凯同学的数学学习小组遇到一个富有挑战性的探宄问题，请你帮助他们完成整个探究过程；

    （问题背景）

    对于一个正整数n，我们进行如下操作：

    （1）将n拆分为两个正整数m1，m2的和，并计算乘积m1×m2；

    （2）对于正整数m1，m2，分别重复此操作，得到另外两个乘积；

    （3）重复上述过程，直至不能再拆分为止，（即折分到正整数1）；

    （4）将所有的乘积求和，并将所得的数值称为该正整数的“神秘值”，

    请探究不同的拆分方式是否影响正整数n的“神秘值”，并说明理由．

    （尝试探究）：

    （1）正整数1和2的“神秘值”分别是

    （2）为了研究一般的规律，小凯所在学习小组通过讨论，决定再选择两个具体的正整数6和7，重复上述过程

    探究结论：

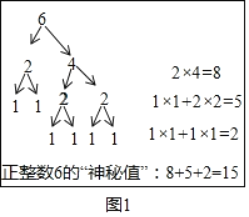
    如图所示，是小凯选择的一种拆分方式，通过该拆分方法得到正整数6的“神秘值”为15．

    请模仿小凯的计算方式，在如图中，选择另外一种拆分方式，给出计算正整数6的“神秘值”的过程；对于正整数7，请选择一种拆分方式，在如图中绐出计算正整数7的“神秘值”的过程．

    （结论猜想）

    结合上面的实践活动，进行更多的尝试后，小凯所在学习小组猜测，正整数n的“神秘值”与其折分方法无关．请帮助小凯，利用尝试成果，猜想正整数n的“神秘值”的表达式为 ，（用含字母n的代数式表示，直接写出结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算

    （1）（+11）+（﹣12）﹣（+18）

    （2）2.25+（+0.75）﹣（+2）+（﹣1.75）

    （3）﹣17÷×（﹣9）

    （4）（﹣3）2﹣[（﹣12）×（﹣）+（﹣2）3]

    查看答案和解析>>

    同步练习册答案