
 在一次抓捕贩毒分子的行动中,一贩毒分子从两条公路的交点O处沿到两条公路OM、ON距离相等的一条小路上逃窜(如图所示,在∠MON内),埋伏在A、B两处的公安人员想在相等的距离同时抓住贩毒分子(两处公安人员速度相同),请你帮助公安人员在图中标出抓捕点P的位置(不写作法,保留作图痕迹).
在一次抓捕贩毒分子的行动中,一贩毒分子从两条公路的交点O处沿到两条公路OM、ON距离相等的一条小路上逃窜(如图所示,在∠MON内),埋伏在A、B两处的公安人员想在相等的距离同时抓住贩毒分子(两处公安人员速度相同),请你帮助公安人员在图中标出抓捕点P的位置(不写作法,保留作图痕迹).  通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ACB=60°,分别以△ABC的两边向形外作等边△BCE、等边△ACF,过A作AM∥FC交BC于点M,连接EM,求证:AB=ME.
如图,△ABC中,∠ACB=60°,分别以△ABC的两边向形外作等边△BCE、等边△ACF,过A作AM∥FC交BC于点M,连接EM,求证:AB=ME.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m
如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
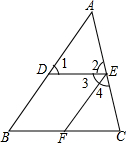 如图,在三角形ABC中,D、E分别是AB、AC边上的点,∠A=50°,∠1=60°,∠4=50°,∠BFE=120°.
如图,在三角形ABC中,D、E分别是AB、AC边上的点,∠A=50°,∠1=60°,∠4=50°,∠BFE=120°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com