
 如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m
如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m分析 (1)作DE⊥AC于点E,根据sinC=$\frac{DE}{CD}$即可得DE;
(2)由∠C=45°可得CE,由tan∠EAD=$\frac{DE}{AE}$可得AE,即可得AC的长,再在Rt△ABC中,根据sinC=$\frac{AB}{AC}$即可得AB的长.
解答 解:(1)如图,作DE⊥AC于点E,
再Rt△CDE中,sinC=$\frac{DE}{CD}$,
∴$\frac{\sqrt{2}}{2}$=$\frac{DE}{8}$,
∴DE=4$\sqrt{2}$,
答:点D到CA的距离为4$\sqrt{2}$;
(2)在Rt△CDE中,∠C=45°,
∴△CDE为等腰直角三角形,
∴CE=DE=4$\sqrt{2}$,
∵∠ADB=75°,∠C=45°,
∴∠EAD=∠ADB-∠C=30°,
∴在Rt△ADE中,tan∠EAD=$\frac{DE}{AE}$,
∴$\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{2}}{AE}$,
∴AE=4$\sqrt{6}$,
∴AC=AE+CE=4$\sqrt{6}$+4$\sqrt{2}$,
在Rt△ABC中,sinC=$\frac{AB}{AC}$,
∴$\frac{\sqrt{2}}{2}$=$\frac{AB}{4\sqrt{6}+4\sqrt{2}}$,
∴AB=4+4$\sqrt{3}$,
答:旗杆AB的高为(4+4$\sqrt{3}$)m.
点评 本题考查了解直角三角形,用到的知识点是仰角的定义、特殊角的三角函数值,要能借助仰角构造直角三角形并解直角三角形.


科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,DE⊥AB于点D,交AC于点E.
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,DE⊥AB于点D,交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一次抓捕贩毒分子的行动中,一贩毒分子从两条公路的交点O处沿到两条公路OM、ON距离相等的一条小路上逃窜(如图所示,在∠MON内),埋伏在A、B两处的公安人员想在相等的距离同时抓住贩毒分子(两处公安人员速度相同),请你帮助公安人员在图中标出抓捕点P的位置(不写作法,保留作图痕迹).
在一次抓捕贩毒分子的行动中,一贩毒分子从两条公路的交点O处沿到两条公路OM、ON距离相等的一条小路上逃窜(如图所示,在∠MON内),埋伏在A、B两处的公安人员想在相等的距离同时抓住贩毒分子(两处公安人员速度相同),请你帮助公安人员在图中标出抓捕点P的位置(不写作法,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,某地汽车站、火车站分别位于A、B两点,直线m和n分别表示公路与铁路.
如图所示,某地汽车站、火车站分别位于A、B两点,直线m和n分别表示公路与铁路.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,原点为O,点A(0,3),B(2,3),C(2,-3),D(0,-3).点P,Q是长方形ABCD边上的两个动点,BC交x轴于点M.点P从点O出发以每秒1个单位长度沿O→A→B→M的路线做匀速运动,同时点Q也从点O出发以每秒2个单位长度沿O→D→C→M的路线做匀速运动.当点Q运动到点M时,两动点均停止运动.设运动的时间为t秒,四边形OPMQ的面积为S.
如图,在平面直角坐标系中,原点为O,点A(0,3),B(2,3),C(2,-3),D(0,-3).点P,Q是长方形ABCD边上的两个动点,BC交x轴于点M.点P从点O出发以每秒1个单位长度沿O→A→B→M的路线做匀速运动,同时点Q也从点O出发以每秒2个单位长度沿O→D→C→M的路线做匀速运动.当点Q运动到点M时,两动点均停止运动.设运动的时间为t秒,四边形OPMQ的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
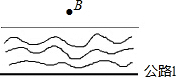 如图,河边有一条笔直的公路l,公路两侧是平坦的草地,在数学活动课上,老师要求测量河对岸B点到公路的距离,请你设计一个测量方案.要求:
如图,河边有一条笔直的公路l,公路两侧是平坦的草地,在数学活动课上,老师要求测量河对岸B点到公路的距离,请你设计一个测量方案.要求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com