
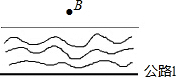
 如图,河边有一条笔直的公路l,公路两侧是平坦的草地,在数学活动课上,老师要求测量河对岸B点到公路的距离,请你设计一个测量方案.要求:
如图,河边有一条笔直的公路l,公路两侧是平坦的草地,在数学活动课上,老师要求测量河对岸B点到公路的距离,请你设计一个测量方案.要求:分析 (1)利用解直角三角形的应用得出测量所使用的测量工具;
(2)结合解直角三角形的应用的方法得出基本解题步骤;
(3)首先表示出AC,AD的长,进而得出B点到CD的距离.
解答  解:(1)测量所使用的测量工具为:量角器、尺子;
解:(1)测量所使用的测量工具为:量角器、尺子;
(2)测量示意图如图所示:
步骤:
①在公路上取两点C、D,使∠BCD、∠BDC为锐角;
②用量角器测出∠BCD=α,∠BDC=β;
③用尺子测得CD的长,记为m米;
④计算求值.
(3)设B点到CD的距离为x米,作BA⊥CD于点A.
在Rt△CAB中,x=CA?tan α;
在Rt△DAB中,x=AD?tan β
∴CA=$\frac{x}{tanα}$,AD=$\frac{x}{tanβ}$
又∵CA+AD=m
∴$\frac{x}{tanα}$+$\frac{x}{tanβ}$=m,
即:x=$\frac{m•tanα•tanβ}{tanα+tanβ}$.
点评 此题主要考查了应用设计与作图,正确掌握解直角三角形的方法是解题关键.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m
如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
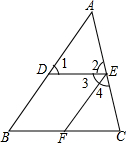 如图,在三角形ABC中,D、E分别是AB、AC边上的点,∠A=50°,∠1=60°,∠4=50°,∠BFE=120°.
如图,在三角形ABC中,D、E分别是AB、AC边上的点,∠A=50°,∠1=60°,∠4=50°,∠BFE=120°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com