
【题目】下图为水平放置于桌面上的台灯的示意图,已知灯臂AB=18cm,灯罩BC=30cm,∠BAM=60°,∠ABC=90°,求点C到桌面的距离CD(精确到0.1cm).参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73.
≈1.73.
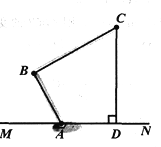
【答案】点C到桌面的距离CD约为30.6 cm.
【解析】
过点B作BE⊥CD于E,过点A作AF⊥BE于点F,根据题意可得∠FBA=∠BAM=60°,∠CBE=30°,在Rt△ABF中,根据![]() ,求得AF,在Rt△BCE中,根据
,求得AF,在Rt△BCE中,根据![]() ,求得CE,然后根据CD=CE+DE=CE+AF即可得解.
,求得CE,然后根据CD=CE+DE=CE+AF即可得解.
如图,过点B作BE⊥CD于E,过点A作AF⊥BE于点F,

∵AD∥BE,
∴∠FBA=∠BAM=60°,
∵∠ABC=90°,
∴∠CBE=90°-∠FBA=30°,
在Rt△ABF中,
∵![]() ,
,
∴![]() =18
=18![]()
![]()
![]() ,
,
在Rt△BCE中,
∵![]() ,
,
∴![]() =30
=30![]()
![]() =15,
=15,
∴CD=CE+DE=CE+AF=![]()
![]() (cm).
(cm).
答:点C到桌面的距离CD约为30.6 cm.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一货轮在A处测得灯塔P在货轮的北偏西23°的方向上,随后货轮以80海里/时的速度按北偏东30°的方向航行,1小时后到达B处,此时又测得灯塔P在货轮的北偏西68°的方向上,求此时货轮距灯塔P的距离PB.(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市高铁站将于今年年底使用,计划在广场内种植A、B两种花木共2000棵,若种植A种花木的数量比种植B种花木数量的3倍多400棵.
(1)求种植A、B两种花木的数量分别是多少棵?
(2)如果园林处安排12人同时种植这两种花木,每人每天能种植A种花木40棵或B种花木30棵,应分别安排多少人种植A种花木和B种花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
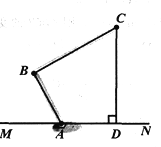
【题目】下图为水平放置于桌面上的台灯的示意图,已知灯臂AB=18cm,灯罩BC=30cm,∠BAM=60°,∠ABC=90°,求点C到桌面的距离CD(精确到0.1cm).参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73.
≈1.73.
查看答案和解析>>
科目:初中数学 来源: 题型:
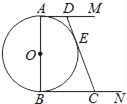
【题目】如图,⊙O的直径AB=2,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN于C.设AD=x,BC=y.
(1)求证:AM∥BN;
(2)求y关于x的关系式;
(3)求四边形ABCD的面积S,并证明:S≥2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简![]() ;
;
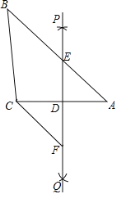
(2)如图,已知△ABC,按如下步骤作图:
①分别以A,C为圆心,大于![]() AC的长为半径画弧,两弧交于P, Q两点;
AC的长为半径画弧,两弧交于P, Q两点;
②作直线PQ,分别交AB,AC于点E,D;
③过C作CF∥AB交PQ于点F.
求证:△AED≌△CFD;
查看答案和解析>>
科目:初中数学 来源: 题型:
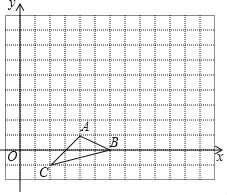
【题目】(1)将△ABC沿x轴负方向平移2个单位,沿y轴正方向平移4个单位,得到△A1B1C1,请画出△A1B1C1.
(2)将△ABC绕点A顺时针旋转90°,得到△AB2C2,请画出△AB2C2.
(3)△A1B1C1绕点P顺时针旋转90°,得到△AB2C2,则点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]() .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,
求两次摸 出都是红球的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com