
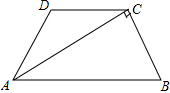
 如图,在等腰梯形ABCD中,AB∥CD,AC⊥BC,∠B=60°,AB=6,则CD的长是3.
如图,在等腰梯形ABCD中,AB∥CD,AC⊥BC,∠B=60°,AB=6,则CD的长是3. 分析 由等腰梯形的性质,可得∠DAB=∠B=60°,又由AC⊥BC,可得∠ACB=90°,从而证得∠CAB=30°,利用直角三角形的性质,即可得到BC=AD=$\frac{1}{2}$AB=3,∠DAC=30°,再由CD∥AB,利用平行线的性质,可得∠DCA=∠CAB=30°,所以∠DAC=∠DCA,可证CD=AD=BC=3.
解答 解:∵等腰梯形ABCD,AB∥CD,∠B=60°
∴∠DAB=∠B=60°,AD=BC,
∵AC⊥BC,
∴∠ACB=90°,
∴∠CAB=30°,
∴∠DAC=30°,
∵AB=6,
∴BC=AD=$\frac{1}{2}$AB=3,
∵CD∥AB,
∴∠DCA=∠CAB=30°,
∴∠DAC=∠DCA,
∴CD=AD=BC=3.
故答案为:3.
点评 本题主要考查了等腰三角形的性质,平行线的性质,直角三角形的性质及等腰三角形的判定,证得CD=AD是解题的关键.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 1.56×10-6米 | B. | 1.56×10-5米 | C. | 0.156×10-7米 | D. | 1.56×10-8米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
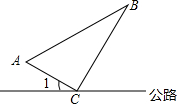 如图,在公路的同侧有A、B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5km/h,问多长时间后这人距离B送奶站最近?
如图,在公路的同侧有A、B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5km/h,问多长时间后这人距离B送奶站最近?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com