Question

某宾馆有50个房间供游客住宿，当每个房间的房价为每天180元时，房间会全部住满．当每个房间每天的房价每增加10元时，就会有一个房间空闲．宾馆需对游客居住的每个房间每天支出20元的各种费用．根据规定，每个房间每天的房价不得高于340元．设每个房间的房价增加x元（x为10的正整数倍）．

（1）设一天订住的房间数为y，直接写出y与x的函数关系式及自变量x的取值范围；

（2）设宾馆一天的利润为w元，求w与x的函数关系式；

（3）一天订住多少个房间时，宾馆的利润最大？最大利润是多少元？

 

Answer 1

（1）y=50-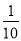x（0＜x≤160，且x为10的正整数倍）；

（2）w=-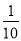x2+34x+8000；

（3）一天订住34个房间时，宾馆每天利润最大，最大利润为10880元；

【解析】

试题分析：（1）用一共有的房间减去房价增长减少的房间数即可；

（2）利用房间数乘每一间房间的利润即可；

（3）利用（2）的函数解析式，配方法求得最大值即可．

试题解析：（1）y=50-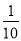x（0＜x≤160，且x为10的正整数倍）；

（2）w=（50-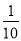x）（180+x-20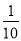）=-x2+34x+8000；

（3）w=-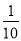x2+34x+8000=-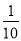（x-170）2+10890

抛物线的对称轴是：x=-=170，抛物线的开口向下，当x＜170时，w随x的增大而增大，

但0＜x≤160，因而当x=160时，即房价是340元时，利润最大，此时一天订住的房间数是：50-=34间，最大利润是：10880元．

答：一天订住34个房间时，宾馆每天利润最大，最大利润为10880元．

考点：二次函数的应用