
(本题满分6分)我市2014年中考的体育考试项目和实验考试项目采用抽签方式决定,规定:实验抽考测密度、欧姆定律、二氧化碳制取三个实验项目中的一个(用纸签A、B、C表示)。体育中考的跳绳、篮球运球投篮、立定跳远三个项目(用纸签D、E、F表示)抽取一项进行考试。在看不到纸签的情况下,分别从中各随机抽取一个.
(1)用“列表法”或“树状图法”表示所有可能出现的结果;
(2)聪聪抽到B和F(记作事件M)的概率是多少?
(1)树状图详见解析;(2)由树状图可知,P(M)=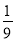
【解析】
试题分析:(1)实验抽考测密度、欧姆定律、二氧化碳制取有三种可能性,体育中考的跳绳、篮球运球投篮、立定跳远也有三种可能性,共有期3×3=9种可能性,利用列表法可或树形图可求出.
(2)看聪聪家长抽到B和F的情况数占总情况数的多少即可
试题解析:(1)方法一:列表格如下:
| D跳绳 | E篮球运球投篮 | F立定跳远 |
A密度 | (A,D) | (A,E) | (A,F) |
B欧姆定律 | (B,D) | (B,E) | (B,F) |
C二氧化碳制取 | (C,D) | (C,E) | (C,F) |
方法二:画树状图如下:
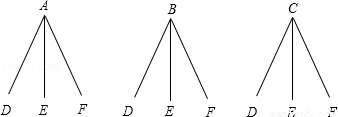
所有可能出现的结果AD AE AF BD BE BF CD CE CF
(2)从表格或树状图可以看出,所有可能出现的结果共有9种,其中事件M出现了一次,所以P(M)=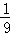
考点:列表法与树状图法


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年浙江省嘉兴市八年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,在△ABC中,DE是AC的中垂线,AD=5,BD=2,则BC的长是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省嘉兴市九年级上学期期中考试数学试卷(解析版) 题型:填空题
若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-m的图象上的三点,则y1,y2,y3的大小关系是__________________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省宁波市九年级10月月考数学试卷(解析版) 题型:选择题
二次函数 的图象的顶点坐标是 ( )
的图象的顶点坐标是 ( )
A.(-1,3) B.(1,3)
C.(1,-3) D.(-1,-3)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省宁波市九年级10月月考数学试卷(解析版) 题型:选择题
已知二次函数 (a<0)的图像过点(1,0)和(
(a<0)的图像过点(1,0)和( ),且-2<
),且-2< <-1,下列5个判断中,① b<0 ②b-a<0 ③a>b-1 ④a<
<-1,下列5个判断中,① b<0 ②b-a<0 ③a>b-1 ④a< ⑤2a<b+
⑤2a<b+ ,正确的是( )
,正确的是( )
A.①③ B.①②③ C.①②③⑤ D.①③④⑤
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省宁波市九年级10月月考数学试卷(解析版) 题型:解答题
(本题满分12分)某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中 .准备在形如Rt
.准备在形如Rt 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:
品种 | 红色花草 | 黄色花草 | 紫色花草 |
价格(元/米2) | 60 | 80 | 120 |
设 的长为
的长为 米,正方形
米,正方形 的面积为
的面积为 平方米,买花草所需的费用为
平方米,买花草所需的费用为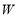 元,解答下列问题:
元,解答下列问题:
(1) 与
与 之间的函数关系式为
之间的函数关系式为 ;
;
(2)求 与
与 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元;
(3)当买花草所需的费用最低时,求 的长.
的长.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省宁波市部九年级上学期第一次月考数学试卷(解析版) 题型:选择题
已知二次函数y=3(x-1)2+k的图象上有三点A( ,y1),B(2,y2),C(﹣
,y1),B(2,y2),C(﹣ ,y3)则
,y3)则 的大小关系为( )
的大小关系为( )
A.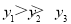 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省宁波市部九年级上学期第一次月考数学试卷(解析版) 题型:解答题
某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省富阳市共同体九年级10月月考数学试卷(解析版) 题型:解答题
如图所示,在平面直角坐标系 中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在
中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在 轴的负半轴和
轴的负半轴和 轴的正半轴上,抛物线
轴的正半轴上,抛物线 经过点A、B,且18
经过点A、B,且18 +
+ =0.
=0.

(1)求抛物线的解析式;
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
① 移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围;
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com