练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，以△ABC中AB、AC边分别向外作正方形ADEB、ACHF，连接DC、BF，试猜测：
    （1）CD与BF相等吗？请说明理由。
    （2）CD⊥BF吗？请说明理由。
    （3）利用旋转的观点：在此图中，△ADC可以看作是△（     ）绕旋转中心（    ）点，按（     ）方向旋转（    ）（填旋转角）得到的。
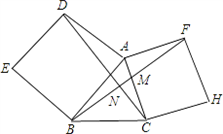    解：
    （1）DC=BF．
    理由：在正方形ABDE中，AD=AB，∠DAB=90°，又在正方形ACHF中，AF=AC，∠FAC=90°， ∴∠DAB=∠FAC=90°，
    ∵∠DAC=∠DAB+∠BAC， ∠FAB=∠FAC+∠BAC，
    ∴∠DAC=∠FAB，
    ∴△DAC≌△FAB，
    ∴DC=FB。
    （2）∵△ABF和△ADC可以通过旋转而相互得到，旋转中心是A，旋转角为90°，
    ∴BF⊥CD。
    （3）根据正方形的性质可得：AD=AB，AC=AF， ∠DAB=∠CAF=90°，
    ∴∠DAC=∠BAF=90°+∠BAC，
    ∴△DAC≌△BAF（SAS），故△ABF可看作△ADC绕A点逆时针旋转90°得到。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

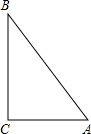    精英家教网如图，Rt△ABC中，∠C=90°，AC=3，AB=5，若以C为圆心，r为半径作圆，那么：
    （1）当直线AB与⊙C相切时，求r的取值范围；
    （2）当直线AB与⊙C相离时，求r的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

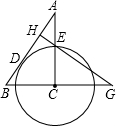    精英家教网如图，在△ABC中，∠ACB=90°，以C为圆心的圆切AB于点D，交AC于点E，过点E作AB的垂线，垂足为H，HE交BC的延长线于点G，已知∠A=α，AE=m，则EG=
     
    （用含α，m的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    26、如图，以△ABC中AB、AC边分别向外作正方形ADEB、ACHF，连接DC、BF，试猜测：
    （1）CD与BF相等吗？请说明理由．
    （2）CD⊥BF吗？请说明理由．
    （3）利用旋转的观点：在此图中，△ADC可以看作是△
    ABF
    绕旋转中心
    A
    点，按
    逆时针
    方向旋转
    90°
    （填旋转角）得到的．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

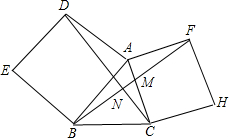    如图，以△ABC中AB、AC边分别向外作正方形ADEB、ACHF，连接DC、BF，试猜测：
    （1）CD与BF相等吗？请说明理由．
    （2）CD⊥BF吗？请说明理由．
    （3）利用旋转的观点：在此图中，△ADC可以看作是△______绕旋转中心______点，按______方向旋转______（填旋转角）得到的．

    查看答案和解析>>

    同步练习册答案