
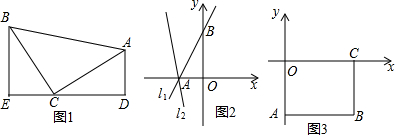
���� ��1�����ݡ�ABCΪ����ֱ�������Σ�AD��ED��BE��ED�����ж���ACD�ա�CBE��
��2���ٹ���B��BC��AB����l2��C����C��CD��y����D�����ݡ�CBD�ա�BAO���ó�BD=AO=3��CD=OB=4�����C��-4��7����������ô���ϵ������ֱ��l2�ĺ�������ʽ��
�ڸ��ݡ�APD���Ե�DΪֱ�Ƕ���ĵ���ֱ�������Σ�����D��ֱ��y=-2x+6�ϵĶ������ڵ�������ʱ�����������������D�ھ���AOCB���ڲ�ʱ������D�ھ���AOCB���ⲿʱ����D��x��-2x+6�����ֱ���ݡ�ADE�ա�DPF���ó�AE=DF���ݴ��г����̽�����⼴�ɣ�
���  �⣺��1��֤������ͼ1���ߡ�ABCΪ����ֱ�������Σ�
�⣺��1��֤������ͼ1���ߡ�ABCΪ����ֱ�������Σ�
��CB=CA����ACD+��BCE=90�㣬
�֡�AD��ED��BE��ED��
���D=��E=90�㣬��EBC+��BCE=90�㣬
���ACD=��EBC��
�ڡ�ACD���CBE�У�
$\left\{\begin{array}{l}��D=��E\\��ACD=��EBC\\ CA=CB\end{array}\right.$��
���ACD�ա�CBE��AAS����
��2������ͼ2������B��BC��AB����l2��C ����C��CD��y����D��
����C��CD��y����D��
�ߡ�BAC=45�㣬
���ABCΪ����ֱ�������Σ�
�ɣ�1����֪����CBD�ա�BAO��
��BD=AO��CD=OB��
��ֱ��l1��y=$\frac{4}{3}$x+4�У���y=0����x=-3����x=0����y=4��
��A��-3��0����B��0��4����
��BD=AO=3��CD=OB=4��
��OD=4+3=7��
��C��-4��7����
��l2�Ľ���ʽΪy=kx+b����
$\left\{\begin{array}{l}{7=-4k+b}\\{0=-3k+b}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-7}\\{b=-21}\end{array}\right.$��
��l2�Ľ���ʽ��y=-7x-21��
��D��4��-2������$\frac{20}{3}��-\frac{22}{3}$����
���ɣ�����D��ֱ��y=-2x+6�ϵĶ������ڵ�������ʱ�������������
����D�ھ���AOCB���ڲ�ʱ����ͼ����D��x���ƽ����EF����ֱ��OA��E����ֱ��BC��F��
��D��x��-2x+6������OE=2x-6��AE=6-��2x-6��=12-2x��DF=EF-DE=8-x��
�ɣ�1���ɵã���ADE�ա�DPF����DF=AE��
����12-2x=8-x��
���x=4��
��-2x+6=-2��
��D��4��-2����
��ʱ��PF=ED=4��CP=6=CB���������⣻
����D�ھ���AOCB���ⲿʱ����ͼ����D��x���ƽ����EF����ֱ��OA��E����ֱ��BC��F��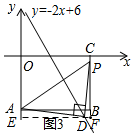
��D��x��-2x+6������OE=2x-6��AE=OE-OA=2x-6-6=2x-12��DF=EF-DE=8-x��
ͬ���ɵã���ADE�ա�DPF����AE=DF��
����2x-12=8-x��
���x=$\frac{20}{3}$��
��-2x+6=-$\frac{22}{3}$��
��D��$\frac{20}{3}$��-$\frac{22}{3}$����
��ʱ��ED=PF=$\frac{20}{3}$��AE=BF=$\frac{4}{3}$��BP=PF-BF=$\frac{16}{3}$��6���������⣮
���� ��������һ�κ����ۺ��⣬��Ҫ�����˵�����ꡢ���ε����ʡ�����ϵ����������ֱ�������ε������Լ�ȫ�������ε����֪ʶ���ۺ�Ӧ�ã��������Ĺؼ����������߹���ȫ�������Σ�����ȫ�������ε����ʽ��м��㣬��Ҫ���ǵĶ������������ʱע�����˼������ã�


 ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��4 | B�� | x��4 | C�� | x��4 | D�� | x��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
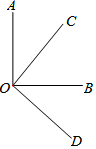 ��ͼ������ֱ�ǡ�AOB����COD����ͬ�Ķ���O�����н��ۣ��١�AOC=��BOD���ڡ�AOC+��BOD=90�㣻����OCƽ�֡�AOB����OBƽ�֡�COD���ܡ�AOD��ƽ�������COB��ƽ������ͬһ�����ߣ�������ȷ�ĸ����У�������
��ͼ������ֱ�ǡ�AOB����COD����ͬ�Ķ���O�����н��ۣ��١�AOC=��BOD���ڡ�AOC+��BOD=90�㣻����OCƽ�֡�AOB����OBƽ�֡�COD���ܡ�AOD��ƽ�������COB��ƽ������ͬһ�����ߣ�������ȷ�ĸ����У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com