
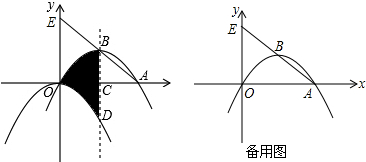
分析 (1)根据平移的性质设出二次函数的解析式,再将点A(8,0)代入即可得解,再根据平移,即可求出阴影部分的面积;
(2)根据两点之间线段最短,以及点O与点A关于l2的对称轴对称,即可求出;
(3)根据三角形相似的条件,进行分类讨论,即可求出本题的答案.
解答 解:(1)设平移后抛物线的解析式y=-$\frac{3}{16}$x2+bx,
将点A(8,0)代入,
得:0=$-\frac{3}{16}×64+8b=0$,
解得:b=$\frac{3}{2}$,∴y=$-\frac{3}{16}{x}^{2}+\frac{3}{2}x$,
顶点B(4,3),
S阴影=OC×CB=4×3=12;
(2)存在,
∵点O与点A关于l2的对称轴对称,
∴连接AE,OF,OF+EF=AE,
此时,点F与点B重合,
∴F(4,3);
(3)存在点P,使得以O、P、M为顶点的三角形与△OAE相似,
设点P(t,$-\frac{3}{16}{t}^{2}+\frac{3}{2}t$) (t≠0),则:OM=|t|,PM=|$-\frac{3}{16}{t}^{2}+\frac{3}{2}t$|,
设直线AB的解析式为:y=kx+b,
把点A(8,0)和B(4,3)代入可得:
$\left\{\begin{array}{l}{8k+b=0}\\{4k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=6}\end{array}\right.$,
∴y=$-\frac{3}{4}x+6$,当x=0时,y=6,
∴E(0,6),
①$\frac{OM}{PM}$=$\frac{OE}{OA}$=$\frac{3}{4}$时,$\frac{|t|}{|-\frac{3}{16}{t}^{2}+\frac{3}{2}t|}$=$\frac{3}{4}$,
∴$\frac{t}{-\frac{3}{16}{t}^{2}+\frac{3}{2}t}$=$\frac{3}{4}$或$-\frac{t}{-\frac{3}{16}{t}^{2}+\frac{3}{2}t}$=$\frac{3}{4}$,
解得:t=$\frac{8}{9}$,或t=$\frac{136}{9}$∴P($\frac{8}{9}$,$-\frac{32}{27}$)或P($\frac{136}{9}$,$-\frac{544}{27}$),
②$\frac{OM}{PM}$=$\frac{OA}{OE}$=$\frac{4}{3}$时,$\frac{|t|}{|-\frac{3}{16}{t}^{2}+\frac{3}{2}t|}$=$\frac{4}{3}$,
∴$\frac{t}{-\frac{3}{16}{t}^{2}+\frac{3}{2}t}$=$\frac{4}{3}$或$-\frac{t}{-\frac{3}{16}{t}^{2}+\frac{3}{2}t}$=$\frac{4}{3}$,
解得:t=4或t=12,∴P(4,3)或P(12,-9),
∴P1(4,3),P2(12,-9),P3($\frac{8}{9}$,$-\frac{32}{27}$),P4($\frac{136}{9}$,$-\frac{544}{27}$)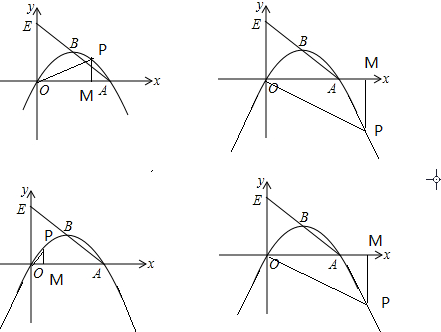 .
.
点评 本题主要考查了用待定系数法求二次函数的解析式,平移的性质,以及利用对称求最值的问题,还考查了判定相似三角形的条件以及分类讨论的思想,是一道综合性很强的题目,要注意总结.


科目:初中数学 来源: 题型:解答题
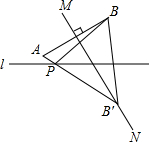 如图,已知点B关于直线l的对称点是B′,AB的垂直平分线MN交BB′于B′,AB′交直线l于点P,点B到直线l的距离为3cm,求PA+PB的值.
如图,已知点B关于直线l的对称点是B′,AB的垂直平分线MN交BB′于B′,AB′交直线l于点P,点B到直线l的距离为3cm,求PA+PB的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{8}}{3}$ | B. | $\frac{{2\sqrt{2}}}{{\sqrt{9}}}$ | C. | $\frac{2}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
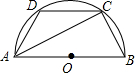 如图,AB是半圆O的直径,D是$\widehat{AC}$上一点,若∠BAC=35°,则∠ADC的度数是( )
如图,AB是半圆O的直径,D是$\widehat{AC}$上一点,若∠BAC=35°,则∠ADC的度数是( )| A. | 100° | B. | 120° | C. | 125° | D. | 130° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:| 类别 | 人数 | 占总人数比例 |
| 重视 | a | b |
| 一般 | 57 | 0.285 |
| 不重视 | c | 0.36 |
| 说不清楚 | 9 | 0.045 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com