
【题目】如图,在 Rt△ABC 中,∠ABC=90°,AB=BC=![]() ,将△ABC 绕点 C 逆时针旋转 60°,得到△MNC, 连接 BM,则 BM 的长是 .
,将△ABC 绕点 C 逆时针旋转 60°,得到△MNC, 连接 BM,则 BM 的长是 .

【答案】![]() .
.
【解析】试题分析:首先考虑到BE所在的三角形并不是特殊三角形,所以猜想到要求BE,可能需要构造直角三角形.由旋转的性质可知,AC=AE,∠CAE=60°,故△ACE是等边三角形,可证明△ABE与△CBE全等,可得到∠ABE=45°,∠AEB=30°,再证△AFB和△AFE是直角三角形,然后在根据勾股定理求解
解:连结CE,设BE与AC相交于点F,如下图所示,
∵Rt△ABC中,AB=BC,∠ABC=90°
∴∠BCA=∠BAC=45°
∵Rt△ABC绕点A逆时针旋转60°与Rt△ADE重合,
∴∠BAC=∠DAE=45°,AC=AE
又∵旋转角为60°
∴∠BAD=∠CAE=60°,
∴△ACE是等边三角形
∴AC=CE=AE=4
在△ABE与△CBE中,![]()
∴△ABE≌△CBE (SSS)
∴∠ABE=∠CBE=45°,∠CEB=∠AEB=30°
∴在△ABF中,∠BFA=180°﹣45°﹣45°=90°
∴∠AFB=∠AFE=90°
在Rt△ABF中,由勾股定理得,
BF=AF=![]() =2
=2
又在Rt△AFE中,∠AEF=30,°∠AFE=90°
FE=AF=2
∴BE=BF+FE=2+2
故,本题的答案是:2+2



 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】教材中有如下一段文字:
思考
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC,固定住长木棍,转动短木棍,得到△ABD,这个实验说明了什么?
如图中的△ABC与△ABD满足两边和其中一边的对角分别相等,即AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等.这说明,有两边和其中一边的对角分别相等的两个三角形不一定全等.
小明通过对上述问题的再思考,提出:两边分别相等且这两边中较大边所对的角相等的两个三角形全等.请你判断小明的说法 . (填“正确”或“不正确”)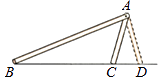
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
老舍先生曾说“天堂是什么样子,我不晓得,但从我的生活经验去判断,北平之秋便是天堂.”(摘自《住的梦》)金黄色的银杏叶为北京的秋增色不少.
小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树.他先让爸爸开车驶过这段公路,发现速度为60千米/小时,走了约3分钟,由此估算这段路长约千米.
然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米.小宇计划从路的起点开始,每a米种一棵树,绘制示意图如下:
考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵树,请你求出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”假期.某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点.再从B点沿斜坡BC到达山巅C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°,点C到水平线AM的距离为600米.
(1)求B点到水平线AM的距离.
(2)求斜坡AB的坡度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com