
【题目】定义:数学活动课上,乐老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.
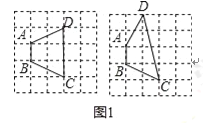
理解:(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请在方格图中画出以格点为顶点,AB、BC为边的两个对等四边形ABCD;
(2)如图2,在圆内接四边形ABCD中,AB是⊙O的直径,AC=BD.求证:四边形ABCD是对等四边形;
(3)如图3,点D、B分别在x轴和y轴上,且D(8,0),B(0,6),点A在BD 边上,且AB=2.试在x轴上找一点C,使ABOC是对等四边形,请直接写出所有满足条件的C点坐标.
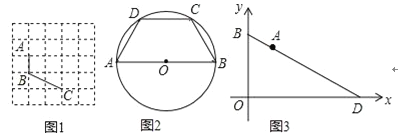
【答案】(1)四边形ABCD为对等四边形,图见解析;
(2)四边形ABCD是对等四边形;
(3)C点坐标为:(2,0)或(![]() ,0).
,0).
【解析】
试题分析:(1)根据对等四边形的定义画出图形即可;
(2)根据圆周角定理得到∠ADB=90°,∠ACD=90°,根据直角三角形全等的判定定理证明Rt△ADB≌Rt△BCA,根据全等三角形的性质证明即可;
(3)分OC=AB、AC=OB两种情况,根据平行线分线段成比例定理计算即可.
试题解析:(1)如图1:四边形ABCD为对等四边形;
(2)证明:∵AB是⊙O的直径,
∴∠ADB=90°,∠ACD=90°,
在Rt△ADB和Rt△BCA中,
![]() ,
,
∴Rt△ADB≌Rt△BCA,
∴AD=BC,
∴四边形ABCD是对等四边形;
(3)∵D(8,0),B(0,6),
∴OD=8,OB=6,∴BD=10,
∵AB=2,∴AD=8,
如图3,当OC=AB时,C点坐标为(2,0),

如图4,当AC=OB时,AC=6,
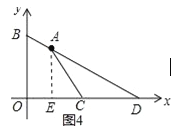
作AE⊥OD于E,
则AE∥OB,
∴![]() ,即
,即![]() ,
,
解得![]() ,DE=
,DE=![]() ,
,
∴![]() ,
,
OE=OD﹣DE=![]() ,
,
则OC=OE+EC=![]() ,
,
∴C点坐标为(![]() ,0),
,0),
∴四边形ABOC为对等四边形时,C点坐标为:(2,0)或(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】从泰州到某市,可乘坐普通列车或动车,已知动车的行驶路程是400千米,普通列车的行驶路程是动车的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若动车的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐动车所需时间比乘坐普通列车所需时间缩短3小时,求动车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
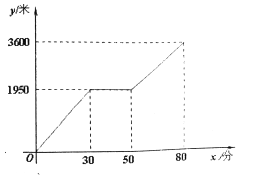
【题目】小颖和小亮上山游玩,小颗乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颗在小亮出发后50分才乘上缆车,缆车的平均速度为180米/分,设小亮出发x分后行走的路程为y米。图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是_________米,他途中休息了___________分;
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度;
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为 人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是 ;
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有 人.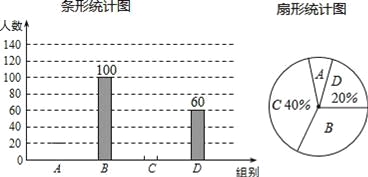
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com