Question

1．如图，PA，PB是圆O的切线，切点分别为A，B，若点C位圆O上一点．
（1）若∠APB=40°，则∠ACB的度数为70°．
（2）若∠APB=α°，则∠ACB的度数为90°-$\frac{1}{2}$α．

Answer 1

分析 连接OA、OB，如图，先根据切线的性质得∠OAP=∠OBP=90°，再根据四边形内角和得到∠AOB=180°-∠P，则根据圆周角定理得到∠ACB=$\frac{1}{2}∠$AOB=90°-$\frac{1}{2}$∠P，
（1）把∠APB=40°代入∠ACB=90°-$\frac{1}{2}$∠P计算即可；
（2）把∠APB=α代入∠ACB=90°-$\frac{1}{2}$∠P即可．

解答 解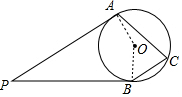：连接OA、OB，如图，
∵PA，PB是圆O的切线，
∴OA⊥AP，OB⊥PB，
∴∠OAP=∠OBP=90°，
∴∠P+∠AOB=180°，
即∠AOB=180°-∠P，
∴∠ACB=$\frac{1}{2}∠$AOB=90°-$\frac{1}{2}$∠P，
（1）当∠APB=40°，∠ACB=90°-$\frac{1}{2}$×40°=70°；
（2）∠APB=α°，∠ACB=90°-$\frac{1}{2}$α．
故答案为70°，90°-$\frac{1}{2}$α．

点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．