
����Ŀ��Ϊ�ˡ��������ˮ���̡�ij�������Ӵ��˶Կ�����Ⱦ���������ȣ����������Ŭ���������������Ը��ƣ����ռ��˸�������30��Ŀ������������Ϊ���������������������±����һ��������������ͳ��ͼ��

˵����������������ָ����AQI�������涨������50ʱ����������Ϊ�ţ�51������100ʱ����������Ϊ����101������150ʱ����������Ϊ�����Ⱦ��151������200ʱ����������Ϊ�ж���Ⱦ����
����������Ϣ������������⣺
��1��ֱ��д��������Ⱦָ���������ݵ����� ����λ�� ��
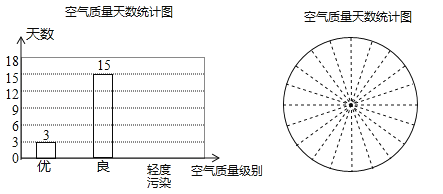
��2���벹ȫ����������������ͳ��ͼ��
��3����������ɵ�����ͳ��ͼ��������Ӧ������ͳ��ͼ��
��4������ר����ܰ��ʾ��������Ⱦָ����100�����ʺ��������˶��������������Ϣ�����Ƹ��о���һ�꣨��365��ƣ����ж������ʺ��������˶���
���𰸡���1��90��90����2����ͼ����������3����ͼ����������4��219��
��������
�����������1�����������Ķ���Ϳ��Եó��������ݵ�����Ϊ90����30�����������ڵ�15�͵�16��������ƽ�����Ϳ��Եó���λ��Ϊ90��
��2������ͳ�Ʊ������ݷֱ��������š����������Ⱦ��ʱ�伴�ɣ�
��3��������ͳ��ͼ�ֱ������š����������Ⱦ�İٷֱȼ�Բ�ĽǵĶ������ɣ�
��4�������30���п�����Ⱦָ����100���µı�ֵ�����������ֵ����365��Ϳ���������ۣ�
�����������1��������������90���ֵĴ������7�Σ����������ݵ�����Ϊ90���������������������м����������90��90������������ƽ������90�������������ݵ���λ����90��
�ʴ�Ϊ��90��90��
��2�������⣬�������Ⱦ������Ϊ��30��3��15=12�죮
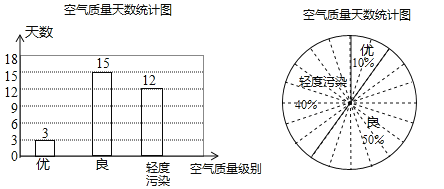
��3�������⣬������ռ��Բ�ĽǵĶ���Ϊ��3��30��360=36�㣬����ռ��Բ�ĽǵĶ���Ϊ��15��30��360=180�㣬�����Ⱦ��ռ��Բ�ĽǵĶ���Ϊ��12��30��360=144����
��4�����о���һ�꣨��365��ƣ������ʺ��������˶�������Ϊ��18��30��365=219�죮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������⣺�ٶԶ�����ȣ����ڴ�����ȣ���ͬλ����ȣ���ֱ��ƽ�У���0����������0��������ѭ��С����������������������ĸ���Ϊ�� ��
A.2
B.3
C.4
D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪��������һ��������n�����Խ��������ķֽ⣺n=p��q��p��q������������p��q������n���������ַֽ��У����p��q������֮��ľ���ֵ��С�����Ǿͳ�p��q��n����ѷֽ⣮���涨��F��n��=![]() ��
��
����12���Էֽ��1��12��2��6��3��4����Ϊ12��1��6��2��4��3������3��4��12����ѷֽ⣬����F��12��=![]() ��
��
��1�����һ��������m������һ��������n��ƽ�������dz�������m����ȫƽ������
��֤��������һ����ȫƽ����m������F��m��=1��
��2�����һ����λ������t��t=10x+y��1��x��y��9��x��yΪ��Ȼ�������������λ�ϵ�����ʮλ�ϵ����õ���������ȥԭ������λ���������õIJ�Ϊ36����ô���dz������tΪ�����������������С�����������
��3���ڣ�2�����á����������У���F��t�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪����ͼ�٣��ı���ABCD��CEFG��Ϊ�����Σ���֪BE=DG�� ����չ����ͼ�ڣ��ı���ABCD��CEFG��Ϊ���Σ��ҡ�A=��F����֤��BE=DG��
��Ӧ�á���ͼ�ۣ��ı���ABCD��CEFG��Ϊ���Σ���E�ڱ�AD�ϣ���G��AD�ӳ����ϣ���AE=2ED����A=��F����EBC�����Ϊ8��������CEFG�����Ϊ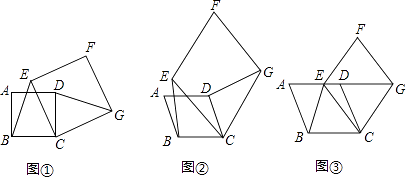
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijС����ͥ�õ������С����������˸�С��n����ͥ2017��4�µ��õ������õ��������ݶ��������������������������Ƴ�Ƶ���ֲ�ֱ��ͼ��ͼ����ʾ�� 
��1����n��ֵ��
��2��С�����������ݰ�ÿ���õ���x���ȣ���С��Ϊ�������ٵ͵���121��x��160�����е���161��x��200���۸ߵ���201��x��240�������Ƴ�����ͳ��ͼ��ͼ����ʾ���������������ͳ��ͼ����������
��3���õ����Ծ����õ�ʵ�С������շѡ����涨���õ���������200�Ȱ���һ���ݵ���շѣ�����200�ȵIJ��ְ��ڶ����ݵ���շѣ��������ϵ�����������2017��4�¸�С��300����ͥ������һ���ݵ���շѶ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������ε��ڽǺ���360�������������εı���Ϊ��������
A. 6 B. 5 C. 4 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽��
��ͼ��������![]() ��
��![]() �ύ��A��B���㣨��A�ڵ�B����ࣩ����
�ύ��A��B���㣨��A�ڵ�B����ࣩ����![]() �ύ�ڵ�C������AC��BC����P��AC��ÿ��1����λ���ȵ��ٶ��ɵ�A���C�˶���ͬʱ����Q��BO��ÿ��2����λ���ȵ��ٶ��ɵ�B���O�˶�����һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶�������PQ������Q��QD��x�ᣬ�������߽��ڵ�D����BC���ڵ�E������PD����BC���ڵ�F�����P���˶�ʱ��Ϊ
�ύ�ڵ�C������AC��BC����P��AC��ÿ��1����λ���ȵ��ٶ��ɵ�A���C�˶���ͬʱ����Q��BO��ÿ��2����λ���ȵ��ٶ��ɵ�B���O�˶�����һ����ֹͣ�˶�ʱ����һ����Ҳ��ֹ֮ͣ�˶�������PQ������Q��QD��x�ᣬ�������߽��ڵ�D����BC���ڵ�E������PD����BC���ڵ�F�����P���˶�ʱ��Ϊ![]() �루
�루![]() ����
����
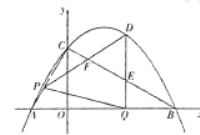
��1����ֱ��BC�ĺ�������ʽ��
��2����ֱ��д��P��D��������꣨�ú�![]() �Ĵ���ʽ��ʾ������軯��
�Ĵ���ʽ��ʾ������軯��
���ڵ�P��Q�˶��Ĺ����У���PQ=PDʱ����![]() ��ֵ��
��ֵ��
��3����̽���ڵ�P��Q�˶��Ĺ����У��Ƿ����ijһʱ�̣�ʹ�õ�FΪPD���е㣮�����ڣ���ֱ��д����ʱ![]() ��ֵ���F�����ꣻ�������ڣ���˵�����ɣ�
��ֵ���F�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ���ʦ������Զ�ɼ��������ǣ� ��
A. ����ȷ��һ��ֱ��B. ����֮�䣬�߶����
C. ���߶����D. ƽ����ľ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��y��z����y��z��x��+z��x��y���������ȷ���ǣ� ��
A.2xy��2yz
B.��2yz
C.xy��2yz
D.2xy��xz
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com