
【题目】综合与探究
如图,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与![]() 轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ,过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E.连接PD,与BC交于点F.设点P的运动时间为
轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ,过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E.连接PD,与BC交于点F.设点P的运动时间为![]() 秒(
秒(![]() ).
).
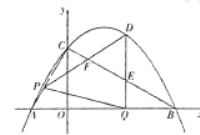
(1)求直线BC的函数表达式.
(2)①直接写出P、D两点的坐标(用含![]() 的代数式表示,结果需化简).
的代数式表示,结果需化简).
②在点P、Q运动的过程中,当PQ=PD时,求![]() 的值.
的值.
(3)试探究在点P、Q运动的过程中,是否存在某一时刻,使得点F为PD的中点.若存在,请直接写出此时![]() 的值与点F的坐标;若不存在,请说明理由.
的值与点F的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①P(
;(2)①P(![]() ,
,![]() ),D(
),D(![]() ,
,![]() );②
);②![]() ;(3)t=3,F(
;(3)t=3,F(![]() ,
,![]() ).
).
【解析】
试题分析:(1)先求出B、C两点的坐标,进而求出直线BC的函数表达式;
(2)①过点P作PG⊥x轴于点G ,由AO=3,BO=9,OC=![]() ,得到∠CAO=60°,∠APG=30°,从而有AP=t, AG=
,得到∠CAO=60°,∠APG=30°,从而有AP=t, AG=![]() ,PG=
,PG=![]() ,得到P的坐标.由OQ=
,得到P的坐标.由OQ=![]() ,得到D的横坐标,由D在抛物线上,得到D的纵坐标;
,得到D的横坐标,由D在抛物线上,得到D的纵坐标;
②过点P作PG⊥x轴于点G,PH⊥QD于点H,得到四边形PGQH是矩形,从而有QD=2HQ=2PG,解关于t的方程即可;
(3)由中点坐标公式和F在直线BC上得到![]() ,解得t=3.把t=3代入得到F的坐标.
,解得t=3.把t=3代入得到F的坐标.
试题解析:(1)由y=0,得![]() ,解得:
,解得:![]() ,
,![]() ,∴点A的坐标为(-3,0),点B的坐标为(9,0).由x=0,得
,∴点A的坐标为(-3,0),点B的坐标为(9,0).由x=0,得![]() ,∴点C的坐标为(0,
,∴点C的坐标为(0,![]() ).
).
设直线BC的函数表达式为:![]() ,∴
,∴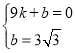 ,解得:
,解得: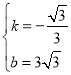 ,∴直线BC的函数表达式为:
,∴直线BC的函数表达式为:![]() ;
;
(2)①过点P作PG⊥x轴于点G .∵A(-3,0),B(9,0),C(0,![]() )∴AO=3,BO=9,OC=
)∴AO=3,BO=9,OC=![]() ,∴tan∠CAO=
,∴tan∠CAO=![]() ,∴∠CAO=60°,∴∠APG=30°,∵AP=t,∴AG=
,∴∠CAO=60°,∴∠APG=30°,∵AP=t,∴AG=![]() ,PG=
,PG=![]() ,∴OG=3-
,∴OG=3-![]() ,∴P(
,∴P(![]() ,
,![]() ).∵OQ=
).∵OQ=![]() ,∴D的横坐标为
,∴D的横坐标为![]() ,∵D在抛物线
,∵D在抛物线![]() 上,∴D的纵坐标为
上,∴D的纵坐标为![]() =
=![]() ,∴D D(
,∴D D(![]() ,
,![]() ).
).
综上所述:P(![]() ,
,![]() ),D(
),D(![]() ,
,![]() );
);
②过点P作PG⊥x轴于点G,PH⊥QD于点H.∵QD⊥x轴,∴四边形PGQH是矩形,∴HQ=PG.∵PQ=PD,PH⊥QD,∴QD=2HQ=2PG.
∵P、D两点的坐标分别为P(![]() ,
,![]() ),D(
),D(![]() ,
,![]() ),∴
),∴![]() =
=![]() ,解得:
,解得:![]() (舍去),
(舍去),![]() ,∴当PQ=PD时,t的值为
,∴当PQ=PD时,t的值为![]() .
.
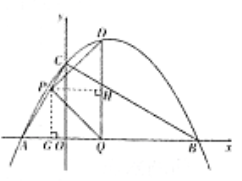
(3)∵F为PD的中点,且P(![]() ,
,![]() ),D(
),D(![]() ,
,![]() ),由中点坐标公式得:F(
),由中点坐标公式得:F(![]() ,
,![]() ),∵F在直线BC上,∴
),∵F在直线BC上,∴![]() ,∴
,∴![]() ,解得:t=3.
,解得:t=3.
当t=3时,![]() =
=![]() ,
,![]() =
=![]() ,∴F(
,∴F(![]() ,
,![]() ).
).


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:当温度达到设定温度![]() 时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到
时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到![]() 时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至
时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至![]() 时,制冷再次停止,……,按照以上方式循环进行.
时,制冷再次停止,……,按照以上方式循环进行.
同学们记录了44![]() 内15个时间点冷柜中的温度
内15个时间点冷柜中的温度![]() 随时间
随时间![]() 的变化情况,制成下表:
的变化情况,制成下表:
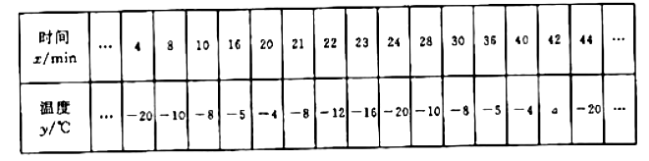
(1)通过分析发现,冷柜中的温度![]() 是时间
是时间![]() 的函数.
的函数.
①当![]() 时,写出一个符合表中数据的函数解析式 ;
时,写出一个符合表中数据的函数解析式 ;
②当![]() 时,写出一个符合表中数据的函数解析式 ;
时,写出一个符合表中数据的函数解析式 ;
(2)![]() 的值为 ;
的值为 ;
(3)如图,在直角坐标系中,已描出了上表中部分数据对应的点,请描出剩余对应的点,并画出![]() 时温度
时温度![]() 随时间
随时间![]() 变化的函数图象.
变化的函数图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数![]() (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
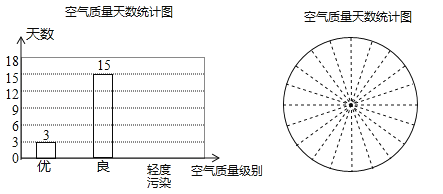
【题目】为了“天更蓝,水更绿”某市政府加大了对空气污染的治理力度,经过几年的努力,空气质量明显改善,现收集了该市连续30天的空气质量情况作为样本,整理并制作了如下表格和一幅不完整的条形统计图:

说明:环境空气质量指数(AQI)技术规定:ω≤50时,空气质量为优;51≤ω≤100时,空气质量为良;101≤ω≤150时,空气质量为轻度污染;151≤ω≤200时,空气质量为中度污染,…
根据上述信息,解答下列问题:
(1)直接写出空气污染指数这组数据的众数 ,中位数 ;
(2)请补全空气质量天数条形统计图:
(3)根据已完成的条形统计图,制作相应的扇形统计图;
(4)健康专家温馨提示:空气污染指数在100以下适合做户外运动,请根据以上信息,估计该市居民一年(以365天计)中有多少天适合做户外运动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是__________(只填序号).
①有理数分为正数和负数;②所有的有理数都能用数轴上的点表示;③符号不同的两个数互为相反数;④两数相加,和一定大于任何一个加数;⑤两数相减,差一定小于被减数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com