
【题目】如图,在等边△BCD中,DF⊥BC于点F,点A为直线DF上一动点,以B为旋转中心,把BA顺时针方向旋转60°至BE,连接EC.
(1)当点A在线段DF的延长线上时,
①求证:DA=CE;
②判断∠DEC和∠EDC的数量关系,并说明理由;
(2)当∠DEC=45°时,连接AC,求∠BAC的度数.

【答案】(1)①证明见解析②∠DEC+∠EDC=90°;(2)150°或30°
【解析】试题分析: ![]() ①证明△BAD≌△BEC,即可证明.
①证明△BAD≌△BEC,即可证明.
②分别求出![]() 和
和![]() 的度数,即可求出∠DEC和∠EDC的数量关系.
的度数,即可求出∠DEC和∠EDC的数量关系.
![]() 分三种情况进行讨论.
分三种情况进行讨论.
试题解析:
(1)①证明:∵把BA顺时针方向旋转60°至BE,
∴![]() 60°,
60°,

![]() 在等边△BCD中,
在等边△BCD中,
![]() ,
, ![]()
![]() ,
,
![]() ,
,
![]() ,
,
∴△BAD≌△BEC,
∴DA=CE;
②判断:∠DEC+∠EDC=90°.
![]() ,
, ![]() ,
, ![]() ,
,
∵△BAD≌△BEC,
∴∠BCE=∠BDA=30°,
![]() 在等边△BCD中,∠BCD=60°,
在等边△BCD中,∠BCD=60°,
∴∠DCE=∠BCE+∠BCD=90°,∴∠DEC+∠EDC=90°.
(2)分三种情况考虑:
①当点A在线段DF的延长线上时(如图1),
由(1)可得, ![]() 是直角三角形,
是直角三角形, ![]() ,
,
当![]() 时,
时,
![]() ,
,
![]() ,
, ![]() ,
,
由(1)得DA=CE,∴CD=DA,在等边![]() 中,
中, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
![]() .
.
②当点A在线段DF上时(如图2),
以B为旋转中心,把BA顺时针旋转![]() 至BE.
至BE.
![]() ,
,

在等边![]() 中,
中, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
在![]()
![]() ,
,
![]() <
<![]() ,
,
∵DA<DF,DA=CE,
∴CE<DC,
由②可知![]() 为直角三角形,
为直角三角形,
∴∠DEC≠45°.
③当点A在线段FD的延长线上时(如图3),

同第②种情况可得![]() ≌
≌![]() ,
,
![]() ,
,
在等边![]() 中,
中, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,
![]() ,
,
![]() ,
,
![]() ,
,
∴AD=CD=BD,
∵![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
综上所述, 的度数是
![]() 或
或![]()


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
(1)求证:四边形PMAN是正方形;
(2)求证:EM=BN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上的一点,DA与⊙O相切于点A,DA=DC=![]() .
.

(1)求证:DC是⊙O的切线;
(2)若∠CAB=30°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
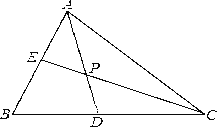
【题目】如图,△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,AD、CE相交于点P
(1) 求∠CPD的度数
(2) 若AE=3,CD=7,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“五·一车展”期间,某汽车经销商推出![]() 四种型号的轿车共1000辆进行展销,
四种型号的轿车共1000辆进行展销,![]() 型号轿车销售的成交率(售出数量
型号轿车销售的成交率(售出数量![]() 展销数量)为50%,图1是各型号参展轿车的百分比,图2是已售出的各型号轿车的数量,(两幅统计图尚不完整)
展销数量)为50%,图1是各型号参展轿车的百分比,图2是已售出的各型号轿车的数量,(两幅统计图尚不完整)

(1)参加展销的![]() 型号轿车有多少辆?
型号轿车有多少辆?
(2)请你将图2的统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了推动球类运动的普及,成立多个球类运动社团,为此,学生会采取抽样调查的方法,从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好(要求每位同学只能选择其中一种自己喜欢的球类运动),并将调查结果绘制成了如下条形统计图和扇形统计图(不完整).请你根据图中提供的信息,解答下列问题:

(1)本次抽样调查,共调查了 名学生;
(2)请将条形统计图和扇形统计图补充完整;
(3)若该学校共有学生1800人,根据以上数据分析,试估计选择排球运动的同学约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
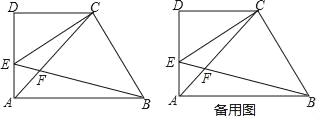
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮与小明做投骰子(质地均匀的正方体)的实验与游戏.
(1)在实验中他们共做了50次试验,试验结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 10 | 9 | 6 | 9 | 8 | 8 |
填空:此次实验中,“1点朝上”的频率是 ;
② 小亮说:“根据试验,出现1点朝上的概率最大.”他的说法正确吗?为什么?
(2)小明也做了大量的同一试验,并统计了“1点朝上”的次数,获得的数据如下表:
试验总次数 | 100 | 200 | 500 | 1000 | 2000 | 5000 | 10000 |
1点朝上的次数 | 18 | 34 | 82 | 168 | 330 | 835 | 1660 |
1点朝上的频率 | 0.180 | 0.170 | 0.164 | 0.168 | 0.165 | 0.167 | 0.166 |
“1点朝上”的概率的估计值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com