
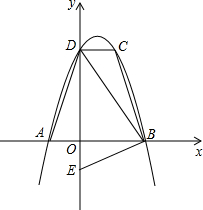
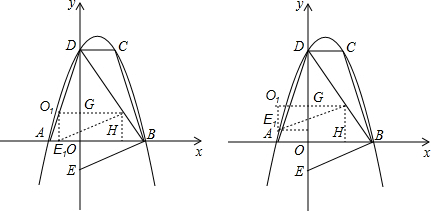
 x+c�ϣ����е�A��B��x���ϣ���D��y���ϣ���CD��AB����֪S����ABCD=8��tan��DAO=4����B������Ϊ��2��0������E����Ϊ��0��-1����
x+c�ϣ����е�A��B��x���ϣ���D��y���ϣ���CD��AB����֪S����ABCD=8��tan��DAO=4����B������Ϊ��2��0������E����Ϊ��0��-1���� ����λÿ����ٶ���BD���յ�D�����˶������˶�ʱ��Ϊ
����λÿ����ٶ���BD���յ�D�����˶������˶�ʱ��Ϊ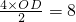 ��
��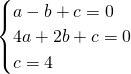 ��
��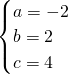 ��
�� t��B1O1=2��B1H=2t��BH=t��
t��B1O1=2��B1H=2t��BH=t��
 ��
�� t��B1H=2 t��BH=t��
t��B1H=2 t��BH=t��
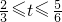 ��
�� ��
�� �� ��3��
�� ��3�� �� ��-1��
�� ��-1�� ����
���� ��2+
��2+ ���Գ���x=
���Գ���x= ��
�� -
- |OE|=
|OE|= -
- =0��x2=
=0��x2= +
+ =1��
=1�� x-1����EE����е�����Ϊ��1��
x-1����EE����е�����Ϊ��1�� ����
���� x+b������1��
x+b������1�� ���������ʽ�ã�b=
���������ʽ�ã�b=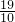 ��
�� x+
x+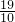 ����y=2ʱ��x=-2��
����y=2ʱ��x=-2�� ��2+
��2+ ����������
���������� ����kB'E'=-2��
����kB'E'=-2��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��ƽ��ֱ������ϵ�У�OΪֱ��������ABC��ֱ�Ƕ��㣬��B=30�㣬��Ƕ���A��˫����y=
��ͼ��ƽ��ֱ������ϵ�У�OΪֱ��������ABC��ֱ�Ƕ��㣬��B=30�㣬��Ƕ���A��˫����y=| 1 | x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 =2
=2| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��ƽ��ֱ������ϵ�У�OB��x���ϣ���ABO=90�㣬��A������Ϊ��1��2��������AOB�Ƶ�A��ʱ����ת90�㣬���O�Ķ�Ӧ��C������Ϊ��������
��ͼ��ƽ��ֱ������ϵ�У�OB��x���ϣ���ABO=90�㣬��A������Ϊ��1��2��������AOB�Ƶ�A��ʱ����ת90�㣬���O�Ķ�Ӧ��C������Ϊ���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| a+2 |
| S��CAD |
| S��DGH |
| AD |
| GH |
| FC+2AE |
| 3AM |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��ƽ��ֱ������ϵ�У�A������Ϊ��8��0����B������Ϊ��0��6��C���߶�AB���е㣮������y�����Ƿ����һ��P��ʹ����P��B��CΪ��������������AOB���ƣ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�
��ͼ��ƽ��ֱ������ϵ�У�A������Ϊ��8��0����B������Ϊ��0��6��C���߶�AB���е㣮������y�����Ƿ����һ��P��ʹ����P��B��CΪ��������������AOB���ƣ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com