
阅读下面学习材料:
已知多项式![]() 有一个因式是
有一个因式是![]() ,求m的值。
,求m的值。
解法一:设![]() =
=![]() ,
,
则![]() =
=![]()
比较系数得: ,解得
,解得 ,所以m=0.5
,所以m=0.5
解法二:设![]() =A
=A![]() (A为整式)。由于上式为恒等式,为了方便计算,取x=-0.5,得
(A为整式)。由于上式为恒等式,为了方便计算,取x=-0.5,得![]() 解得m=0.5
解得m=0.5
根据上面学习材料,解答下面问题:
已知多项式![]() 有因式
有因式![]() 和
和![]() ,试用两种方法求m、n的值。
,试用两种方法求m、n的值。
解法1:
解法2:
 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:阅读理解
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 阅读下面的材料:
阅读下面的材料:查看答案和解析>>
科目:初中数学 来源:2013届北京市西城区(北区)九年级上学期期末考试数学试卷(带解析) 题型:解答题
阅读下面的材料:
小明在学习中遇到这样一个问题:若1≤x≤m,求二次函数 的最大值.他画图研究后发现,
的最大值.他画图研究后发现, 和
和 时的函数值相等,于是他认为需要对
时的函数值相等,于是他认为需要对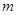 进行分类讨论.
进行分类讨论.
他的解答过程如下:
∵二次函数 的对称轴为直线
的对称轴为直线 ,
,
∴由对称性可知, 和
和 时的函数值相等.
时的函数值相等.
∴若1≤m<5,则 时,
时, 的最大值为2;
的最大值为2;
若m≥5,则 时,
时, 的最大值为
的最大值为 .
.
请你参考小明的思路,解答下列问题:
(1)当 ≤x≤4时,二次函数
≤x≤4时,二次函数 的最大值为_______;
的最大值为_______;
(2)若p≤x≤2,求二次函数 的最大值;
的最大值;
(3)若t≤x≤t+2时,二次函数 的最大值为31,则
的最大值为31,则 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年北京市西城区(北区)九年级上学期期末考试数学试卷(解析版) 题型:解答题
阅读下面的材料:
小明在学习中遇到这样一个问题:若1≤x≤m,求二次函数 的最大值.他画图研究后发现,
的最大值.他画图研究后发现, 和
和 时的函数值相等,于是他认为需要对
时的函数值相等,于是他认为需要对 进行分类讨论.
进行分类讨论.
他的解答过程如下:
∵二次函数 的对称轴为直线
的对称轴为直线 ,
,
∴由对称性可知, 和
和 时的函数值相等.
时的函数值相等.
∴若1≤m<5,则 时,
时, 的最大值为2;
的最大值为2;
若m≥5,则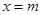 时,
时, 的最大值为
的最大值为 .
.

请你参考小明的思路,解答下列问题:
(1)当 ≤x≤4时,二次函数
≤x≤4时,二次函数 的最大值为_______;
的最大值为_______;
(2)若p≤x≤2,求二次函数 的最大值;
的最大值;
(3)若t≤x≤t+2时,二次函数 的最大值为31,则
的最大值为31,则 的值为_______.
的值为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com