
分析 (1)直接去括号,再按照绝对值的定义进行计算即可;
(2)分四种情况进行讨论:表示x的点在2的右边,-5和2之间,-5的左边,即①当x>2时,②当x=2时,③当-5<x<2时,④当x=-5时,分别计算;
(3)当x表示的点在2时,它到-5、到2、到4的距离和最小,代入计算即可.
解答 解:(1)|5-(-2)|=|5+2|=7,
故答案为:7;
(2)|x+5|+|x-2|=7,
分四种情况:①当x>2时,等式变形为:x+5+x-2=7,
x=2,
②当x=2时,等式变形为:2+5=7,7=7,等式成立;
③当-5<x<2时,等式变形为:x+5+2-x=7,7=7,等式成立;
∵x是整数,
∴x=-4、-3、-2、-1、0、1,
④当x=-5时,等式变形为:0+|-5-2|=7,7=7,等式成立;
综上所述,当x=-5、-4、-3、-2、-1、0、1、2时,|x+5|+|x-2|=7成立;
(3)由题意得:当x=2时,|x+5|+|x-2|+|x-4|的和最小
则|x+5|+|x-2|+|x-4|=2+5+0+|2-4|=7+2=9.
点评 本题考查了数轴上两点的距离与绝对值的关系,两数差的绝对值可以利用有理数法则进行计算,也可以利用数轴上两点的距离进行计算,本题比较难理解,可以利用数形结合方法解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
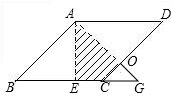 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AGE,那么△AGE与四边形AECD重叠部分的面积是多少?
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AGE,那么△AGE与四边形AECD重叠部分的面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
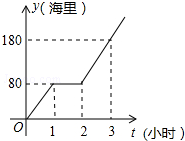 diaoyudao自古就是中国领土,中国政府已对钓鱼开展常态化巡逻.某人,为按计划准点到达指定海拔,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,求该巡逻艇原计划准点到的时间.
diaoyudao自古就是中国领土,中国政府已对钓鱼开展常态化巡逻.某人,为按计划准点到达指定海拔,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,求该巡逻艇原计划准点到的时间.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.
如图所示,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com