
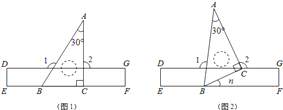
����Ŀ����ͼ1����һ�麬30����ֱ�����ǰ�ABC��BC�߷����ڳ�����ֱ��DEFG��EF���ϣ�
��1����գ���1= �㣬��2= �㣻
��2���ְ����ǰ���B����ʱ����תn�㣮
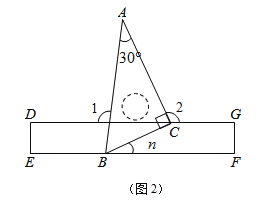
����ͼ2����0��n��90���ҵ�Cǡ������DG����ʱ�����1����2�Ķ���������ú�n�Ĵ���ʽ��ʾ����
�ڵ�0��n��360ʱ���Ƿ��������ǰ�ijһ�����ڵ�ֱ����ֱ�ߣ��������ߣ�ijһ�����ڵ�ֱ�ߴ�ֱ��������ڣ�ֱ��д������n��ֵ�Ͷ�Ӧ�����������ߣ���������ڣ�˵�����ɣ�
���𰸡���1��120��90��(2) �١�1=180�㩁n�㣬��2=90��+n�㣻�ڼ�������
����������������1�������ڲ��ǵĶ����ƽ���ߵ����ʽ����
��2�������ڲ��ǵĶ��������ABE���ٸ�����ֱ��ƽ����ͬλ����ȿɵá�1=��ABE��������ֱ��ƽ����ͬ���ڽǻ��������BCG��Ȼ������ܽǵ���360�����㼴�ɵõ���2��
��3�����ͼ������AB��BC��AC��������ֱ�ߴ�ֱ������⣮
�������1����1=180�㩁60��=120�㣬��2=90�㣻
�ʴ�Ϊ��120��90��
��2������ͼ2��
�ߡ�ABC=60�㣬���ABE=180�㩁60�㩁n��=120�㩁n�㣮
��DG��EF�����1=��ABE=120�㩁n�㣬��BCG=180�㩁��CBF=180�㩁n�㣮
�ߡ�ACB+��BCG+��2=360�㣬���2=360�㩁��ACB����BCG=360�㩁90�㩁��180�㩁n�㣩=90��+n�㣻
�ڵ�n=30��ʱ��AB��DG��EF����
��n=90��ʱ��BC��DG��EF����AC��DE��GF����
��n=120��ʱ��AB��DE��GF����
��n=180��ʱ��AC��DG ��EF����BC��DE��GF����
��n=210��ʱ��AB��DG ��EF����
��n=270��ʱ��BC��DG ��EF����AC��DE��GF����
��n=300��ʱ��AB��DE ��GF����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y= ![]() +x+m�Ķ�����ֱ��y=x+3�ϣ�����F����2��2����ֱ�߽����������ڵ�M��N���㣨��M�ڵ�N����ߣ���MA��x���ڵ�A��NB��x���ڵ�B��
+x+m�Ķ�����ֱ��y=x+3�ϣ�����F����2��2����ֱ�߽����������ڵ�M��N���㣨��M�ڵ�N����ߣ���MA��x���ڵ�A��NB��x���ڵ�B��
��1����ͨ���䷽�������ߵĶ������꣨������ú�m�Ĵ���ʽ��ʾ��������m��ֵ��
��2�����N�ĺ�����Ϊa�����ú�a�Ĵ���ʽ��ʾ��N�������꣬��˵��NF=NB��
��3��������NM��x���ڵ�P����PAPB= ![]() �����M�����꣮
�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������Ӧ��������ġ���ɫ��չ����̼���С����٣�ij������������һ���������������г�������֪������3����ʽ������4��Ůʽ����������ͬ������5����ʽ������4��Ůʽ��������16000Ԫ.
(1)����ʽ������Ůʽ�����ĵ��ۣ�
(2)������Ҫ����ʽ����Ůʽ������4�������ֵ���������Ҫ22�����������ֵ����ķ��ò�����50000Ԫ���������м��ֹ��÷������������ò���ʹ�����ܷ�����ͣ���ͷ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���ABC=90�㣬AC=AD��M��N�ֱ�ΪAC��AD���е㣬
�ҡ�ABM=��BAM������BM��MN��BN��
��1����֤��BM=MN��
��2����BAD=60�㣬ACƽ�֡�BAD��AC=2����BN�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ, ![]() ���ܳ�Ϊ36���Խ���AC��BD�ཻ�ڵ�O����E��CD���е�,BD=12�����DOE���ܳ���
���ܳ�Ϊ36���Խ���AC��BD�ཻ�ڵ�O����E��CD���е�,BD=12�����DOE���ܳ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�����ı���ABCD�У�AD��BC��E��F�ֱ���DC��AB�ߵ��е㣬FE���ӳ��߷ֱ���AD��BC���ӳ��߽���H��G�㣮��֤����AHF����BGF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��E��AB���е㣬�Ե�EΪԲ�ģ�EBΪ�뾶��������BC�ڵ�D������ED���ӳ�����F��ʹDF=DE������FC������B=70�������F�Ķ����ǣ�������

A. 40 B. 70 C. 50 D. 45
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�ܵ�ѧУʳ��������A��B������ǰ���Ŷӵ���һ����(��Ϊa�ˣ�a��8������վ��A���ڶ���ĺ��棬����2���ӣ�������A����ÿ������4�����˷��뿪���飬B����ÿ������6�����˷��뿪���飬��B���ڶ������ÿ��������5�ˣ�
��1����ʱ����С�ܼ�����A�����Ŷӣ��������ﴰ��������ʱ���Ƕ��٣����ú�a�Ĵ���ʽ��ʾ��
��2����ʱ����С��Ѹ�ٴ�A���ڶ���ת�Ƶ�B���ں��������Ŷӣ��ҵ���B����������ʱ��ȼ�����A�����Ŷӵ���A����������ʱ���٣���a��ȡֵ��Χ�����������������أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ǹ������¶��壺��һ���ı��ε������Խ�����ȣ��������ı���Ϊ�ȶԽ����ı��Σ������������⣺
��1��д������ѧ���������ı������ǵȶԽ����ı��ε�����ͼ�ε����ƣ�
��2��̽�������ȶԽ����ı����������Խ����������Ϊ60��ʱ�����60�������Ե�����֮��������һ���Խ��ߵĴ�С��ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com