【题目】如图，在△ABC中，AB=AC，E是AB的中点，以点E为圆心，EB为半径画弧，交BC于点D，连接ED并延长到点F，使DF=DE，连接FC，若∠B=70°，则∠F的度数是（ ）
A. 40 B. 70 C. 50 D. 45
阅读快车系列答案科目：初中数学 来源： 题型：
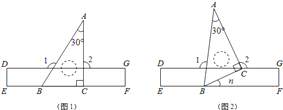
【题目】如图1，把一块含30°的直角三角板ABC的BC边放置于长方形直尺DEFG的EF边上．
（1）填空：∠1= °，∠2= °；
（2）现把三角板绕B点逆时针旋转n°．
①如图2，当0＜n＜90，且点C恰好落在DG边上时，求∠1、∠2的度数（结果用含n的代数式表示）；
②当0＜n＜360时，是否会存在三角板某一边所在的直线与直尺（有四条边）某一边所在的直线垂直？如果存在，直接写出所有n的值和对应的那两条垂线；如果不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商厦进货员在苏州发现了一种应季围巾，用8000元购进一批围巾后，发现市场还有较大的需求，又在上海用17600元购进了同一种围巾，数量恰好是在苏州所购数量的2倍，但每条比在苏州购进的多了4元．问某商厦在苏州、上海分别购买了多少条围巾？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料后解决问题：
小明遇到下面一个问题：
计算（2+1）（22+1）（24+1）（28+1）．
经过观察，小明发现如果将原式进行适当的变形后可以出现特殊的结构，进而可以应用平方差公式解决问题，具体解法如下：（2+1）（22+1）（24+1）（28+1）
=（2+1）（2﹣1）（22+1）（24+1）（28+1）
=（22﹣1）（22+1）（24+1）（28+1）
=（24﹣1）（24+1）（28+1）
=（28﹣1）（28+1）
=216﹣1
请你根据小明解决问题的方法，试着解决以下的问题：
（1）（2+1）（22+1）（24+1）（28+1）（216+1）=_____．
（2）（3+1）（32+1）（34+1）（38+1）（316+1）=_____．
（3）化简：（m+n）（m2+n2）（m4+n4）（m8+n8）（m16+n16）．
查看答案和解析>>
科目：初中数学 来源： 题型：
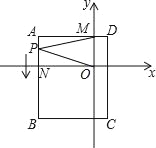
【题目】如图，已知点A（﹣m，n），B（0，m），且m、n满足
+（n﹣5）2=0，点C在y轴上，将△ABC沿y轴折叠，使点A落在点D处．
（1）写出D点坐标并求A、D两点间的距离；
（2）若EF平分∠AED，若∠ACF﹣∠AEF=20°，求∠EFB的度数；
（3）过点C作QH平行于AB交x轴于点H，点Q在HC的延长线上，AB交x轴于点R，CP、RP分别平分∠BCQ和∠ARX，当点C在y轴上运动时，∠CPR的度数是否发生变化？若不变，求其度数；若变化，求其变化范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平面直角坐标系中，ABCD为长方形，其中点A、C坐标分别为（﹣4，2）、（1，﹣4），且AD∥x轴，交y轴于M点，AB交x轴于N．
（1）求B、D两点坐标和长方形ABCD的面积；
（2）一动点P从A出发（不与A点重合），以
个单位/秒的速度沿AB向B点运动，在P点运动过程中，连接MP、OP，请直接写出∠AMP、∠MPO、∠PON之间的数量关系；
（3）是否存在某一时刻t，使三角形AMP的面积等于长方形面积的
？若存在，求t的值并求此时点P的坐标；若不存在请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，两个大小一样的直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到
的位置，AB=12cm，DH=4cm，平移的距离是8cm，则阴影面积是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
