【题目】如图，已知点A（﹣m，n），B（0，m），且m、n满足+（n﹣5）2=0，点C在y轴上，将△ABC沿y轴折叠，使点A落在点D处．

（1）写出D点坐标并求A、D两点间的距离；

（2）若EF平分∠AED，若∠ACF﹣∠AEF=20°，求∠EFB的度数；

（3）过点C作QH平行于AB交x轴于点H，点Q在HC的延长线上，AB交x轴于点R，CP、RP分别平分∠BCQ和∠ARX，当点C在y轴上运动时，∠CPR的度数是否发生变化？若不变，求其度数；若变化，求其变化范围．

参考答案：

【答案】（1）10；（2）20°；（3）∠CPH=45°．理由见解析.

【解析】分析：（1）先由非负数的性质求出m，n的值，得到A点坐标，再根据折叠的性质得点D与点A关于y轴对称，再根据关于y轴对称的点的坐标特征得到D点坐标，然后计算点A与点D的横坐标之差即可得到A、D两点间的距离；

（2）根据折叠的性质得∠DCF=∠ACF，再利用三角形外角性质得∠DCF=∠EFB+∠DEF，则∠EFB=∠ACF-∠DEF，又∠DEF=∠AEF，所以∠EFB=∠ACF-∠AEF=20°；

（3）根据平行线的性质由QH∥AB得到∠QCP=∠1，∠ARX=∠3，再根据角平分线的定义得∠QCP=∠BCQ，∠2=∠ARX，则∠1=∠BCQ，∠2=∠3，接着利用三角形外角性质得∠BCQ=90°+∠3，所以2∠1=90°+2∠2，即∠1=45°+∠2，然根据∠1=∠CPR+∠2即可得到∠CPR=45°．

详解：（1）∵+（n-5）2=0，

∴m+5=0，n-5=0，

∴m=-5，n=5，

∴A点坐标为（5，5），

∵△ABC沿y轴折叠，使点A落在点D处，

∴点D与点A关于y轴对称，

∴D点坐标为（-5，5）；

∴AD=5-（-5）=10；

（2）如图2，

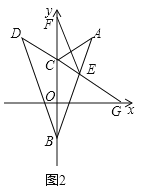
∵△ABC沿x轴折叠，使点A落在点D处，

∴∠DCF=∠ACF，

∵∠DCF=∠EFB+∠DEF，

∴∠EFB=∠ACF-∠DEF，

∵EF平分∠AED，

∴∠DEF=∠AEF，

∴∠EFB=∠ACF-∠AEF=20°；

（3）∠CPH=45°．理由如下：

如图3，

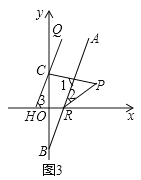
∵QH∥AB，

∴∠QCP=∠1，∠ARX=∠3，

∵CP、RP分别平分∠BCQ和∠ARX，

∴∠QCP=∠BCQ，∠2=∠ARX，

∴∠1=∠BCQ，∠2=∠3，

∵∠BCQ=90°+∠3，

∴2∠1=90°+2∠2，即∠1=45°+∠2，

∵∠1=∠CPR+∠2，

∴∠CPR=45°．

关闭