
【题目】已知△ABC中,∠C=90°,tanA= ![]() ,D是AC上一点,∠CBD=∠A,则sin∠ABD=( )
,D是AC上一点,∠CBD=∠A,则sin∠ABD=( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:作DE⊥AB于点E. ∵∠CBD=∠A,
∴tanA=tan∠CBD= ![]() =
= ![]() ,
,
设CD=1,则BC=2,AC=4,
∴AD=AC﹣CD=3,
在直角△ABC中,AB= ![]() =
= ![]() =2
=2 ![]() ,
,
在直角△ADE中,设DE=x,则AE=2x,
∵AE2+DE2=AD2 ,
∴x2+(2x)2=9,
解得:x= ![]() ,
,
则DE= ![]() ,AE=
,AE= ![]() .
.
∴BE=AB﹣AE=2 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴tan∠DBA= ![]() =
= ![]() ,
,
∴sin∠DBA= ![]() .
.
故选:A.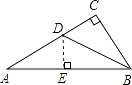
【考点精析】通过灵活运用勾股定理的概念和相似三角形的判定与性质,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.


科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,BD⊥AC于点D,E为BC上一点,过E点作EF⊥AC,垂足为F,过点D作DH∥BC交AB于点H.
(1)请你补全图形。
(2)求证:∠BDH=∠CEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为创建省卫生城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配A、B两种园艺造型共60个,摆放于入城大道的两侧,搭配每个造型所需花卉数量的情况下表所示,结合上述信息,解答下列问题:
造型花卉 | 甲 | 乙 |
A | 80 | 40 |
B | 50 | 70 |
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1500元,试说明选用那种方案成本最低?最低成本为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商厦进货员在苏州发现了一种应季围巾,用8000元购进一批围巾后,发现市场还有较大的需求,又在上海用17600元购进了同一种围巾,数量恰好是在苏州所购数量的2倍,但每条比在苏州购进的多了4元.问某商厦在苏州、上海分别购买了多少条围巾?
查看答案和解析>>
科目:初中数学 来源: 题型:
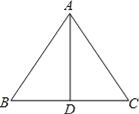
【题目】如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是__.
①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB﹣BD=AC﹣CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(﹣m,n),B(0,m),且m、n满足![]() +(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处.
+(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处.

(1)写出D点坐标并求A、D两点间的距离;
(2)若EF平分∠AED,若∠ACF﹣∠AEF=20°,求∠EFB的度数;
(3)过点C作QH平行于AB交x轴于点H,点Q在HC的延长线上,AB交x轴于点R,CP、RP分别平分∠BCQ和∠ARX,当点C在y轴上运动时,∠CPR的度数是否发生变化?若不变,求其度数;若变化,求其变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求解答下列各题:
(1)解不等式:3x-5<2(2+3x);
(2)解不等式:2x-3≤![]() (x+2);
(x+2);
(3)解不等式: ![]() <x-1,并将解集在数轴上表示出来.
<x-1,并将解集在数轴上表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饮料厂以300千克的A种果汁和240千克的B种果汁为原料,配制生产甲、乙两种新型饮料,已知每千克甲种饮料含0.6千克A种果汁,含0.3千克B种果汁;每千克乙种饮料含0.2千克A种果汁,含0.4千克B种果汁.饮料厂计划生产甲、乙两种新型饮料共650千克,设该厂生产甲种饮料x(千克).
(1)列出满足题意的关于x的不等式组,并求出x的取值范围;
(2)已知该饮料厂的甲种饮料销售价是每1千克3元,乙种饮料销售价是每1千克4元,那么该饮料厂生产甲、乙两种饮料各多少千克,才能使得这批饮料销售总金额最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于P(x,y)作变换得到P′(﹣y+1,x+1),例如:A1(3,1)作上述变换得到A2(0,4),再将A2做上述变换得到A3___________,这样依次得到A1,A2,A3,…An;…,则A2018的坐标为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com