练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．一个反比例函数的图象位于第二、四象限．请你写出一个符合条件的解析式是y=-$\frac{1}{x}$，答案不唯一．

    分析 位于二、四象限的反比例函数比例系数k＜0，据此写出一个函数解析式即可．

    解答 解：∵反比例函数位于二、四象限，
    ∴k＜0，
    解析式为：y=-$\frac{1}{x}$．
    故答案为y=-$\frac{1}{x}$，答案不唯一．

    点评 本题考查了反比例函数的性质，要知道，对于反比例函数y=$\frac{k}{x}$（k≠0），（1）k＞0，反比例函数图象在一、三象限；（2）k＜0，反比例函数图象在第二、四象限内．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

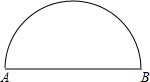    12．小军在为班级办黑板报时遇到了一个难题，在版面设计过程中需将一个半圆面三等分，请你帮助他设计一个合理的等分方案．（要求：不写作法，保留作图痕迹，写出结论．）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．方程$\sqrt{2+x}=x$的解是x=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

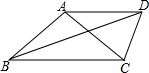    10．如图，等腰△ABC中，AB=AC，∠BAC=100°，BD平分∠ABC，AD∥BC，连接CD，则∠ADC的度数为（　　）
    A．50°B．60°C．70°D．80°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

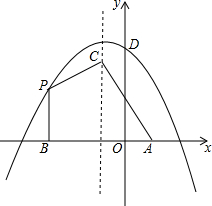    17．如图，平面直角坐标系中，抛物线y=-$\frac{1}{3}$（x+h）2+k的对称轴为x=-1，与y轴交于点D（0，$\frac{13}{3}$）．
    （1）求h和k的值；
    （2）点P为第二象限对称轴左侧抛物线上一点，过P作x轴垂线，垂足为B，点B关于抛物线对称轴的对称点为A，在对称轴上取点C，使∠BPC＞90°，连接AC，若∠BAC=$\frac{1}{2}$∠BPC．求证：PB=PC；
    （3）在（2）条件下，过点A作AE∥PC交抛物线的对称轴于点E，当CE：AE=13：5时，求P点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列命题中正确的个数是（　　）
    ①垂直于弦的直径平分线以及弦所对的两条弧．②平分弦的直径垂直于这条弦，并且平分这条弦所对的两条弧．③弦的垂直平分线经过圆心，并且平分这条弦所对的两条弦．④平分弦所对的一条弧的直径垂直平分这条弦，并且平分这条弦所对的另一条弧．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．利用数轴求不等式组$\left\{\begin{array}{l}{x-1≤0}\\{x＞-3}\end{array}\right.$的解集表示正确的是（　　）
    A．B．C．D．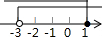

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．某企业接到一批粽子生产任务，按要求在15天内完成，约定这批粽子的出厂价为每只6元，为按时完成任务，该企业招收了新工人，设新工人李明第x天生产的粽子数量为y只，y与x满足下列关系式：
    y=$\left\{\begin{array}{l}{54x}&{（0≤x≤5）}\\{30x+120}&{（5＜x≤15）}\end{array}\right.$．
    （1）李明第几天生产的粽子数量为420只？
    （2）如图，设第x天每只粽子的成本是p元，p与x之间的关系可用图中的函数图象来刻画．若李明第x天创造的利润为w元，求w与x之间的函数表达式，并求出第几天的利润最大，最大利润是多少元？（利润=出厂价-成本）
    （3）设（2）小题中第m天利润达到最大值，若要使第（m+1）天的利润比第m天的利润至少多48元，则第（m+1）天每只粽子至少应提价几元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

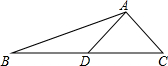    12．如图，AD是△ABC的中线，tanB=$\frac{1}{3}$，cosC=$\frac{\sqrt{2}}{2}$，AC=$\sqrt{2}$．求：
    （1）BC的长；
    （2）sin∠ADC的值．

    查看答案和解析>>

    同步练习册答案