
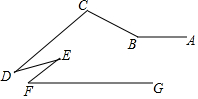
 已知:如图,已知CD∥EF,∠C+∠F=∠ABC,若∠F=a°,a为关于x的一元一次方程$\frac{x-12}{3}$=-$\frac{x-15}{6}$+16的解
已知:如图,已知CD∥EF,∠C+∠F=∠ABC,若∠F=a°,a为关于x的一元一次方程$\frac{x-12}{3}$=-$\frac{x-15}{6}$+16的解分析 (1)分别依据解方程的基本步骤解一元一次方程即可得x的值,即∠F的度数;
(2)如图1,延长AB交CD于点M,延长FE交AM于点N,由CD∥EF知∠1=∠2,根据∠ABC=∠C+∠1且∠C+∠F=∠ABC得∠2=∠F,即可得证;
(3)分以下三种情况求解可得:①如图2,当点P在EF延长线上时;②如图3,延长AB交直线EF于点H,当点P在FH上时;③如图4,当点P在FH的延长线上时.
解答 解:(1)$\frac{x-12}{3}$=-$\frac{x-15}{6}$+16,
2(x-12)=x-15+96
2x-24=-x+15+96
x=4,
即∠F=45°;
(2)如图1,延长AB交CD于点M,延长FE交AM于点N,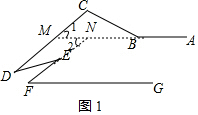
∵CD∥EF,
∴∠1=∠2,
∵∠ABC=∠C+∠1,
∴∠ABC=∠C+∠2,
又∵∠C+∠F=∠ABC,
∴∠2=∠F,
∴AB∥GF;
(3)①如图2,当点P在EF延长线上时,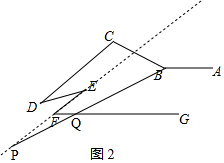
∵∠EFQ=45°,
∴∠PFQ=135°,
∵AB∥GF,
∴∠ABP=∠GQF=∠BPF+∠PFQ,
即∠ABP=∠BPF+135°;
②如图3,延长AB交直线EF于点H,当点P在FH上时,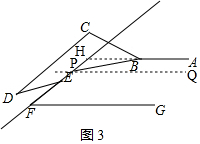
过点P作PQ∥FG,
∵∠EFG=45°,
∴∠FEQ=180°-∠EFG=135°,
则∠BPQ=∠BPF-∠FEQ=∠BPF-135°,
又∵AB∥FG,
∴AB∥PQ,
则∠ABP=180°-∠BPQ=180°-(∠BPF-135°),
即∠ABP=315°-∠BPF;
③如图4,当点P在FH的延长线上时,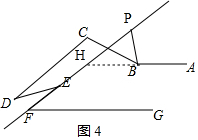
∵AB∥FG,且∠EFG=45°,
∴∠PHB=∠EFG=45°,
∵∠ABP=∠PHB+∠BPF,即∠ABP=45°+∠BPF,
综上,∠ABP=∠BPF+135°或∠ABP=315°-∠BPF或∠ABP=45°+∠BPF.
点评 本题主要考查平行线的判定与性质、三角形外角的性质,熟练掌握平行线的判定与性质是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 点(0,0)是坐标原点 | |
| B. | 对于坐标平面内的任一点,都有唯一的一对有序实数与它对应 | |
| C. | 点A(a,-b )在第二象限,则点B(-a,b)在第四象限 | |
| D. | 若点P的坐标为(a,b),且a•b=0,则点P一定在坐标原点 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3或-3 | B. | 3或-1 | C. | -3或-1 | D. | 3或1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a3•a4=a12 | B. | $\frac{x+3}{{x}^{2}-9}$=$\frac{1}{x-3}$ | C. | (a+2)2=a2+4 | D. | (-xy)3•(-xy)-2=xy |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com