
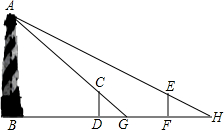
 如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,测得G处、标杆顶端C和建筑物顶端A在同一条直线上;从标杆FE后退4米到点H处,测得H处、标杆顶端E和建筑物顶端A在同一条直线上,AB⊥BH,CD⊥BH,EF⊥BH,求建筑物AB的高.
如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,测得G处、标杆顶端C和建筑物顶端A在同一条直线上;从标杆FE后退4米到点H处,测得H处、标杆顶端E和建筑物顶端A在同一条直线上,AB⊥BH,CD⊥BH,EF⊥BH,求建筑物AB的高. 分析 根据题意可得出△CDG∽△ABG,△EFH∽△ABH,再根据相似三角形的对应边成比例即可得出结论.
解答 解:如图所示:∵AB⊥BH,CD⊥BH,EF⊥BH,
∴AB∥CD∥EF,
∴△CDG∽△ABG,△EFH∽△ABH,
∴$\frac{DC}{AB}$=$\frac{DG}{DG+BD}$,$\frac{EF}{AB}$=$\frac{FH}{FH+DF+DB}$,
∵CD=DG=EF=2m,DF=52m,FH=4m,
∴$\frac{2}{AB}$=$\frac{2}{2+BD}$,$\frac{2}{AB}$=$\frac{4}{4+52+BD}$,
∴$\frac{2}{2+BD}$=$\frac{4}{4+52+BD}$,
解得:BD=52,
∴$\frac{2}{AB}$=$\frac{2}{2+52}$,
解得:AB=54,
答:建筑物AB的高是54m.
点评 本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
 解方程:
解方程:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
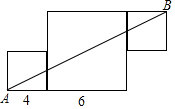 如图,由三个正方形组成一个图形,其中来个正方形的边长分别为4,6,若线段AB将这个圆形分成面积相等的两部分,则第三个正方形的边长为2或4.
如图,由三个正方形组成一个图形,其中来个正方形的边长分别为4,6,若线段AB将这个圆形分成面积相等的两部分,则第三个正方形的边长为2或4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}-1$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com