
 解方程:
解方程:分析 (1)确定a,b,c的值,求出b2-4ac的值,在b2-4ac≥0的前提下,把a、b、c的值代入公式进行计算求出方程的根;
(2)方程两边同除以二次项系数,使二次项系数为1,并把常数项移到方程右边;方程两边同时加上一次项系数一半的平方;把左边配成一个完全平方式,右边化为一个常数;如果右边是非负数,就可以进一步通过直接开平方法来求出它的解;
(3)把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,据此求得黄金比.
解答 解:(1)2x2-5x+1=0
∵a=2,b=-5,c=1,
∴△=25-8=17>0,
∴${x}_{1}=\frac{5+\sqrt{17}}{4}$,${x}_{2}=\frac{5-\sqrt{17}}{4}$;
(2)2x2-4x-1=0
2(x2-2x+1-1)=1,
2(x-1)2-2=1,
2(x-1)2=3,
(x-1)2=$\frac{3}{2}$,
∴x-1=±$\frac{\sqrt{6}}{2}$,
∴${x}_{1}=1+\frac{\sqrt{6}}{2}$,${x}_{2}=1-\frac{\sqrt{6}}{2}$;
(3)设线段AB=1,较长的线段AC的长为x,
∵C是线段AB的黄金分割点,
∴AC2=AB•BC,
x2=1•(1-x),
解得:${x}_{1}=\frac{-1+\sqrt{5}}{2}$,${x}_{2}=\frac{-1-\sqrt{5}}{2}$(舍去负值),
∴$\frac{AC}{AB}$=$\frac{x}{1}$=$\frac{\sqrt{5}-1}{2}$,
答:黄金比为$\frac{\sqrt{5}-1}{2}$.
点评 本题主要考查了运用公式法和配方法解一元二次方程,以及黄金分割,解题时注意:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项,叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:填空题
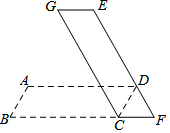 如图,将平行四边形ABCD绕点C顺时针旋转一定角度α(0°<α<180°)后,得到平行四边形EFCG,若BC与CF在同一直线上,且点D恰好在EF上,则α=60°.
如图,将平行四边形ABCD绕点C顺时针旋转一定角度α(0°<α<180°)后,得到平行四边形EFCG,若BC与CF在同一直线上,且点D恰好在EF上,则α=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
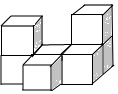 (1)用7个相同的小正方体拼了一个几何体,画出几何体从左面和和上面看到的形状图;
(1)用7个相同的小正方体拼了一个几何体,画出几何体从左面和和上面看到的形状图;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
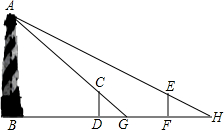 如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,测得G处、标杆顶端C和建筑物顶端A在同一条直线上;从标杆FE后退4米到点H处,测得H处、标杆顶端E和建筑物顶端A在同一条直线上,AB⊥BH,CD⊥BH,EF⊥BH,求建筑物AB的高.
如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,测得G处、标杆顶端C和建筑物顶端A在同一条直线上;从标杆FE后退4米到点H处,测得H处、标杆顶端E和建筑物顶端A在同一条直线上,AB⊥BH,CD⊥BH,EF⊥BH,求建筑物AB的高.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
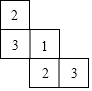 一个几何体由大小相同的小立方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面和左面看到的这个几何体的形状图.
一个几何体由大小相同的小立方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面和左面看到的这个几何体的形状图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com