
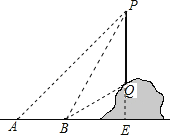
【题目】如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.

(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).
备用数据:![]() ,
,![]() .
.
【答案】(1)∠BPQ=30°;(2)电线杆PQ的高度约9米.
【解析】
试题分析:(1)延长PQ交直线AB于点E,根据直角三角形两锐角互余求得即可;
92)设PE=x米,在直角△APE和直角△BPE中,根据三角函数利用x表示出AE和BE,根据AB=AE﹣BE即可列出方程求得x的值,再在直角△BQE中利用三角函数求得QE的长,则PQ的长度即可求解.
解:延长PQ交直线AB于点E,
(1)∠BPQ=90°﹣60°=30°;
(2)设PE=x米.
在直角△APE中,∠A=45°,
则AE=PE=x米;
∵∠PBE=60°
∴∠BPE=30°
在直角△BPE中,BE=![]() PE=
PE=![]() x米,
x米,
∵AB=AE﹣BE=6米,
则x﹣![]() x=6,
x=6,
解得:x=9+3![]() .
.
则BE=(3![]() +3)米.
+3)米.
在直角△BEQ中,QE=![]() BE=
BE=![]() (3
(3![]() +3)=(3+
+3)=(3+![]() )米.
)米.
∴PQ=PE﹣QE=9+3![]() ﹣(3+
﹣(3+![]() )=6+2
)=6+2![]() ≈9(米).
≈9(米).
答:电线杆PQ的高度约9米.


科目:初中数学 来源: 题型:
【题目】一种袋装大米上标有10±0.3kg,则下列四袋大米中,不符合标准的是( )
袋号 | 一 | 二 | 三 | 四 |
质量/kg | 10.2 | 9.7 | 9.9 | 9.6 |
A、第一袋 B、第二袋 C、第三袋 D、第四袋
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图.
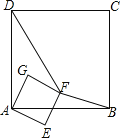
(1)若α=0°,则DF=BF,请加以证明;
(2)试画一个图形(即反例),说明(1)中命题的逆命题是假命题;
(3)对于(1)中命题的逆命题,如果能补充一个条件后能使该逆命题为真命题,请直接写出你认为需要补充的一个条件,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)①如图1,已知AB∥CD,∠ABC=60°,根据 .可得∠BCD= ;
②如图2,在①的条件下,如果CM平分∠BCD,则∠BCM= ;
③如图3,在①、②的条件下,如果CN⊥CM,则∠BCN= .
(2)尝试解决下面问题:已知如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线,CN⊥CM,求∠BCM的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
(1)求线段CD对应的函数表达式;
(2)求E点的坐标,并解释E点的实际意义;
(3)若已知轿车比货车晚出发20分钟,且到达乙地后在原地等待货车,在两车相遇后当货车和轿车相距30千米时,求货车所用时间.

考点:一次函数的应用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com