
【题目】已知:如图所示的一张矩形纸片![]() , 将纸片折叠一次,使点A与C重合,再展开, 折痕EF交AD边于E,交BC边于F,分别连结AF和CE.
, 将纸片折叠一次,使点A与C重合,再展开, 折痕EF交AD边于E,交BC边于F,分别连结AF和CE.
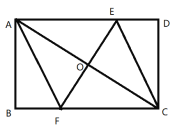
(1)求证:四边形AFCE是菱形;
(2)在线段AC上是否存在一点P,使得![]() ?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
【答案】(1)见解析;(2)存在,过点E作AD的垂线,交AC于点![]() ,点
,点![]() 就是符合条件的点,见解析
就是符合条件的点,见解析
【解析】
(1)由折叠的性质得出EF垂直平分AC,OA=OC,由矩形的性质得出∠B=90°,AD∥BC,得出∠![]() ∠
∠![]() ,∠EAO=∠FCO,由ASA证明△AOE≌△COF,得出AE=CF,证出四边形AFCE是平行四边形,即可得出结论;
,∠EAO=∠FCO,由ASA证明△AOE≌△COF,得出AE=CF,证出四边形AFCE是平行四边形,即可得出结论;
(2)过E作EP⊥AD交AC于P,则P就是所求的点.则∠AEP=90°,证出△AOE∽△AEP,得出对应边成比例![]() ,则AE2=AOAP,再由AO=
,则AE2=AOAP,再由AO=![]() AC,即可得出结论.
AC,即可得出结论.
(1)证明:在矩形ABCD中, AD∥BC
∴ ∠![]() ∠
∠![]() ,∠
,∠![]() =∠
=∠![]()
由折叠可知:OA=OC![]()
∴ △![]() ≌△
≌△![]()
∴ AE=CF,
又AE∥CF
∴ 四边形![]() 是平行四边形
是平行四边形
又由折叠可知:AF=CF,![]()
∴ 四边形![]() 是菱形.
是菱形.
(2)存在,过点E作AD的垂线,交AC于点![]() ,点
,点![]() 就是符合条件的点.
就是符合条件的点.
理由如下:
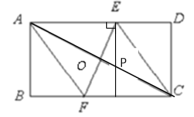
由作法得:∠AEP=90°,
由(1)得:AC⊥EF,
∴∠![]() 90°
90°
∴∠![]() ∠
∠![]() 90°,
90°,
又∵∠![]() ∠
∠![]()
∴ △![]() ∽△
∽△![]()
∴ ![]()
∴AE2=AOAP,
∵AO=![]() AC,
AC,
∴AE2=![]() ACAP
ACAP
即:![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:

下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b![]() )x+c=0的一个根;(4)当
)x+c=0的一个根;(4)当![]() <x<3时,ax2+(b
<x<3时,ax2+(b![]() )x+c>0.其中正确的个数为( )
)x+c>0.其中正确的个数为( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
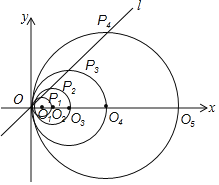
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中![]() 的长为_____.
的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
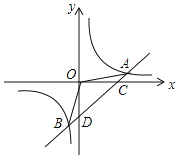
【题目】如图,一次函数y=kx+b(k≠0)和反比例函数y=![]() (m≠0)交于点A(4,1)与点B(﹣1,n).
(m≠0)交于点A(4,1)与点B(﹣1,n).
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等腰三角形,顶角∠BAC=![]() (
(![]() <600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转
<600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转![]() 到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
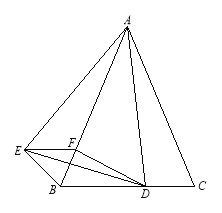
(1)求证:BE=CD
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE,CF.
(1)求证:AF=CE;
(2)若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论.
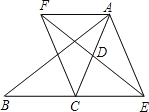
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)

(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,夜晚,小华利用路灯A测量建筑物GF的高度,他在点D处竖立了一根木杆CD,测得木杆CD的影长DE=1.5m,AB⊥EG,CD⊥EG,GF⊥EG.
(1)在图中画出表示建筑物GF影子的线段GH;
(2)已知木杆的高CD=2m,建筑物GF的影子GH=7.8m,木杆CD与路灯杆AB之间的距离BD=5.85m,路灯杆AB与建筑物GF之间的距离BG=6.9m,请你根据题中提供的相关信息,求出建筑物GF的高度.
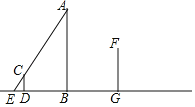
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
![]() 根据上表填空:
根据上表填空:
①抛物线与![]() 轴的交点坐标是________和________;
轴的交点坐标是________和________;
②抛物线经过点![]() ,________
,________![]() ;
;
③在对称轴右侧,![]() 随
随![]() 增大而________;
增大而________;
![]() 试确定抛物线
试确定抛物线![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com