Question

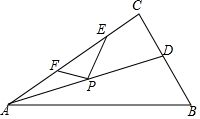
6．如图，Rt△ABC中，AB=10，AC=8，BC=6，∠C=90°，AD平分∠BAC，点E为AC上一点，且AE=3CE，在AC上找一点F，AD上找一点P，连接EP、FP，则EP+FP的最小值为3.6．

Answer 1

分析 如图，作EH⊥AB于H，交AD于G，作F关于AD的对称点F′，连接PF′．因为PF+PE=PE+PF′，根据垂线段最短可知，当F′与H重合，P与G重合时，PE+PF′最短．

解答 解：如图，作EH⊥AB于H，交AD于G，作F关于AD的对称点F′，连接PF′．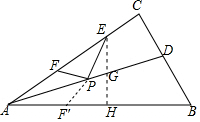

∵PF+PE=PE+PF′，
根据垂线段最短可知，当F′与H重合，P与G重合时，PE+PF′最短．
在Rt△ABC中，AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8，
∵AE=3EC，
∴AE=6，
∵∠EAH=∠BAC，∠EHA=∠C=90°，
∴△AEH∽△ABC，
∴$\frac{EH}{BC}$=$\frac{AE}{AB}$，
∴$\frac{EH}{6}$=$\frac{6}{10}$，
∴EH=3.6，
∴PF+PE的最小值为3.6．
故答案为3.6．

点评 本题考查轴对称-最短问题，角平分线的性质、垂线段最短、相似三角形的判定和性质等知识，解题的关键是学会利用对称，根据垂线段最短解决最值问题，属于中考常考题型．