
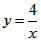 的图象与抛物线
的图象与抛物线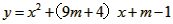 交于点A(3, n)。
交于点A(3, n)。 (x>0)的图象于点C,且AC=2AB,求B、C两点的坐标;
(x>0)的图象于点C,且AC=2AB,求B、C两点的坐标; 
解:(1)∵点A(3, n)在反比例函数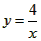 的图象上, 的图象上,∴  ∴A(3, 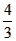 ), ),∵点A(3, 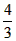 )在抛物线 )在抛物线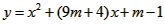 上, 上, ∴ 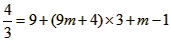 , ,∴ 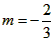 ∴抛物线的解析式为 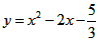 ; ; |
|
| (2)分别过点A、C作x轴的垂线,垂足分别为点D、E, ∴AD∥CE, ∴△ABD∽△CBE, ∴ 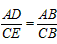 , ,∵AC=2AB, ∴  , ,由题意,得AD= 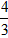 , , ∴ 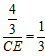 , ,∴CE=4, 即点C的纵坐标为4, 当y=4时,x=1, ∴C(1,4) ∵ 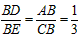 ,DE=2, ,DE=2, ∴ 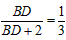 , ,∴BD=1, ∴B(4,0); |
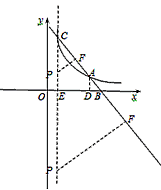 |
(3)∵抛物线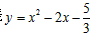 的对称轴是 的对称轴是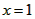 , ,∴P在直线CE 上, 过点P作PF⊥BC于F, 由题意,得PF=PE, ∵∠PCF =∠BCE,∠CFP =∠CEB =90°, ∴△PCF∽△BCE, ∴ 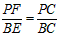 , ,由题意,得BE=3,BC=5, ①当点P在第一象限内时,设P(1,a) (a>0), 则有 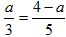 ,解得 ,解得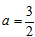 , , ∴点P的坐标为  , ,②当点P在第四象限内时,设P(1,a) (a<0) 则有  ,解得 ,解得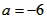 , ,∴点P的坐标为(-1,6), ∴点P的坐标为 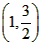 或(-1,6)。 或(-1,6)。 |


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com