
【题目】如图,长方形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上的E点处,折痕的一端G点在边BC上,折痕的另一端F在AD边上且BG=10时.
(1)证明:EF=EG;
(2)求AF的长.

【答案】(1)见解析;(2)6
【解析】
(1)根据翻折的性质可得∠BGF=∠EGF,再根据两直线平行,内错角相等可得∠BGF=∠EFG,从而得到∠EGF=∠EFG,再根据等角对等边证明即可;
(2)根据翻折的性质可得EG=BG,HE=AB,FH=AF,然后在Rt△EFH中,利用勾股定理列式计算即可得解.
证明:(1)∵纸片折叠后顶点B落在边AD上的E点处,
∴∠BGF=∠EGF,
∵长方形纸片ABCD的边AD∥BC,
∴∠BGF=∠EFG,
∴∠EGF=∠EFG,
∴EF=EG;
(2)∵纸片折叠后顶点B落在边AD上的E点处,
∴EG=BG=10,HE=AB=8,FH=AF,
∴EF=EG=10,
∴FH=![]() =
=![]() =6,
=6,
∴AF=FH=6.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】为了解本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷调查(问卷调查表如图所示),并用调查结果绘制了图1,图2两幅统计图(均不完整),请根据统计图解答以下问题:
 (1)本次接受问卷调查的同学有多少人?补全条形统计图.
(1)本次接受问卷调查的同学有多少人?补全条形统计图.
(2)本校有七年级同学800人,估计双休日参加体育锻炼时间在3小时以内(不含3小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且![]() ,弦AD的延长线交切线PC于点E,连接BC.
,弦AD的延长线交切线PC于点E,连接BC.
(1)判断OB和BP的数量关系,并说明理由;
(2)若⊙O的半径为2,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,A(0,4),B(8,0),C(8,4).
(1)试说明四边形AOBC是矩形.
(2)在x轴上取一点D,将△DCB绕点C顺时针旋转90°得到![]() (点
(点![]() 与点D对应).若OD=3,求点
与点D对应).若OD=3,求点![]() 的坐标.
的坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4…
利用你的发现的规律解决下列问题
(1)(a﹣b)(a4+a3b+a2b2+ab3+b4)= (直接填空);
(2)(a﹣b)(an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1)= (直接填空);
(3)利用(2)中得出的结论求62019+62018+…+62+6+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
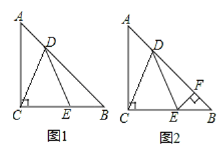
【题目】△ABC中,AC=BC,∠ACB=90°,点D在AB上,E在BC上,且AD=BE,BD=AC.
(1)如图1,求证:DC=DE;
(2)如图2,过E作EF⊥AB于F,若BF=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图I,在![]() 中,
中,![]() .点
.点![]() 在
在![]() 外,连接
外,连接![]() ,作
,作![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() .则
.则![]() 间的等量关系是______;(不用证明)
间的等量关系是______;(不用证明)
(2)如图Ⅱ,![]() ,
,![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,写出
,写出![]() 间的等量关系,并证明你的结论.
间的等量关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com