

分析 首先根据“其它”类所占比例以及人数,进而求出总人数,即可得出喜好“科普常识”的学生人数,再利用样本估计总体得出该年级喜爱“科普常识”的学生总数,进而得出喜好“小说”的人数,以及“漫画”所在扇形的圆心角.
解答 解:①、∵喜欢“其它”类的人数为:30人,扇形图中所占比例为:10%,
∴样本总数为:30÷10%=300(人),
∴喜好“科普常识”的学生有:300×30%=90(人),故此小题正确;
②、若该年级共有1200名学生,则由这两个统计图可估计喜爱“科普常识”的学生约有:$\frac{1200}{300}$×90=360(人),故此小题正确;
③、喜好“小说”的人数为:300-90-60-30=120(人),故此小题错误.
④“漫画”所在扇形的圆心角为:$\frac{60}{300}$×360°=72°,故此小题正确.
故答案为:①②④.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


科目:初中数学 来源: 题型:选择题
| A. | a>-2016 | B. | a<-2016 | C. | a>2016 | D. | a<2016 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (ab-1)(ab+1) | B. | (2x-1)(-1+2x) | C. | (-2x-y)(2x-y) | D. | (-a+5)(-a-5) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
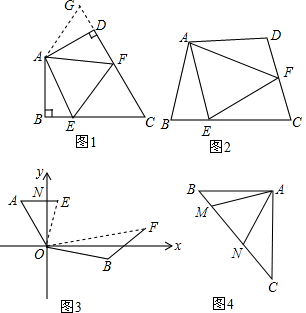
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com