
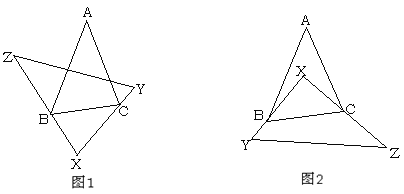
【题目】已知:在△ABC和△XYZ中,∠A=40°,∠Y+∠Z=95°,将△XYZ如图摆放,使得∠X的两条边分别经过点B和点C.
(1)当将△XYZ如图1摆放时,则∠ABX+∠ACX=_____________度;
(2)当将△XYZ如图2摆放时,请求出∠ABX+∠ACX的度数,并说明理由;
(3)能否将△XYZ摆放到某个位置时,使得BX、CX同时平分∠ABC和∠ACB?请直接写出你的结论:___________
【答案】(1)235°;
(2)∠ABX+∠ACX=45°.理由见解析;
(3)不能
【解析】试题分析:(1)要求∠ABX+∠ACX的度数,只要求出∠ABC+∠CBX+∠ACB+∠BCX,利用三角形内角和定理得出∠ABC+∠ACB=180°-∠A=180°-40°=140°;根据三角形内角和定理,∠CBX+∠BCX=∠Y+∠Z=95°,∴∠ABX+∠ACX=∠ABC+∠CBX+∠ACB+∠BCX=140°+95°=235°;(2)要求∠ABX+∠ACX的度数,只要求出∠ABC+∠ACB-(∠BCX+∠CBX)的度数.根据三角形内角和定理,∠CBX+∠BCX=∠Y+∠Z=95°;根据三角形内角和定理得,∠ABC+∠ACB=180°-∠A=140°,∴∠ABX+∠ACX=∠ABC+∠ACB-(∠BCX+∠CBX)=140°-95°=45°;(3)不能.假设能将△XYZ摆放到某个位置时,使得BX、CX同时平分∠ABC和∠ACB.则∠CBX+∠BCX=∠ABX+∠ACX=95°,那么∠ABC+∠ACB=190°,与三角形内角和定理矛盾,所以不能.
试题解析:(1)在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=40°
∴∠ABC+∠ACB=180°40°=140°
在△BCX中,∠X+∠BCX+∠CBX=180°
∴∠BCX+∠CBX=180°∠X
在△XYZ中,∠X+∠Y+∠Z=180°
∴∠Y+∠Z=180°∠X
∴∠CBX+∠BCX=∠Y+∠Z=95°
∴∠ABX+∠ACX=∠ABC+∠CBX+∠ACB+∠BCX=140°+95°=235°;
(2)∠ABX+∠ACX=45度。理由如下:
∵∠Y+∠Z=95°
∴∠X=180°(∠Y+∠Z)=85°
∴∠ABX+∠ACX=180°∠A∠XBC∠XCB=180°40°(180°85°)=45°;
(3)不能。假设能将△XYZ摆放到某个位置时,使得BX、CX同时平分∠ABC和∠ACB.则∠CBX+∠BCX=∠ABX+∠ACX=95°那么∠ABC+∠ACB=190°,与三角形内角和定理矛盾,所以不能。


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式![]() +(b﹣3)2=0,(c﹣4)2≤0
+(b﹣3)2=0,(c﹣4)2≤0

(1)求a、b、c的值;
(2)如果在第二象限内有一点P(﹣m,![]() ),请用含m的式子表示四边形ABOP的面积;
),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在ΔABC和ΔADE中,AB=AC,AD=AE,∠BAC=∠DAE,,且点B,A,D在同一条直线上,连接BE,CD,M,N分别为BE,CD的中点, 连接AM,AN,MN.
⑴.求证:BE=CD
⑵.求证:ΔAMN是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB交CB的延长线于点G.
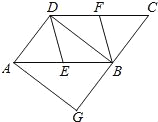
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为: ;
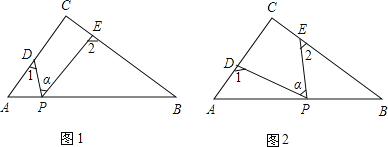
(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.
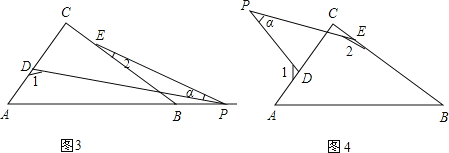
(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
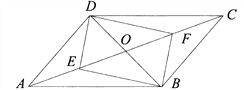
【题目】平行四边形![]() 中,对角线
中,对角线![]() ,
, ![]() 相交于点
相交于点![]() ,若
,若![]() 、
、![]() 是
是![]() 两动点,
两动点, ![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时以2cm/s的相同的速度向
两点同时以2cm/s的相同的速度向![]() 、
、![]() 运动。
运动。
(1)四边形![]() 是平行四边形吗?说明你的理由。
是平行四边形吗?说明你的理由。
(2)若![]() cm,
cm, ![]() cm,当运动时间
cm,当运动时间![]() 为多少时,以
为多少时,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为矩形。
为顶点的四边形为矩形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
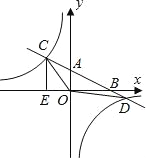
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com