
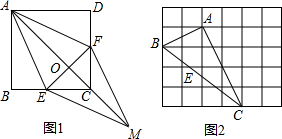
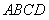 中,点
中,点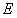 、
、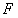 分别是
分别是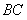 、
、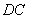 边上的点,且
边上的点,且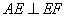 ,
,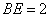
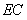 ∶
∶ 的值;
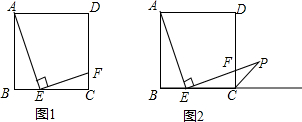
的值;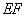 交正方形外角平分线
交正方形外角平分线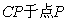 (如图-2),试判断
(如图-2),试判断 的大小关系,并说明理由;
的大小关系,并说明理由; 边上是否存在一点M,使得四边形
边上是否存在一点M,使得四边形 是平行四边形?若存在,请给予证明;若不存在,请说明理由.
是平行四边形?若存在,请给予证明;若不存在,请说明理由. 
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
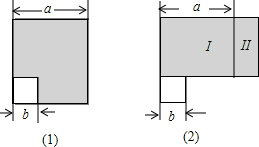 (2012•阜新)如图1,在边长为a的大正方形中剪去一个边长为b的小正方形,再将图中的阴影部分剪拼成一个长方形,如图2.这个拼成的长方形的长为30,宽为20.则图2中Ⅱ部分的面积是
(2012•阜新)如图1,在边长为a的大正方形中剪去一个边长为b的小正方形,再将图中的阴影部分剪拼成一个长方形,如图2.这个拼成的长方形的长为30,宽为20.则图2中Ⅱ部分的面积是查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
| 5 |
| 5 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com